zadanie 32 z matury elle: W układzie współrzędnych punkty A(4,3) i B(10,5) są wierzchołkami trójkąta ABC. Wierzchołek C leży na prostej o równaniu y=2x+3. Oblicz współrzędne punktu C, dla którego kąt ABC jest prosty. Zrobiłam to tak: https://image.ibb.co/cqGug7/IMG_0283.jpg Dlaczego to drugie (zaznaczone) rozwiązanie jest niepoprawne i istnieje tylko jedna opcja?

Gosia: Ponieważ podstawiasz do prostej BC punkt A=(4,3), ale punkt A nie należy do prostej BC.

elle: ale dlaczego muszę podstawić do prostej BC tylko? czemu nie mogę zrobić AC?

elle: a okej, już wiem, żle przeczytałam

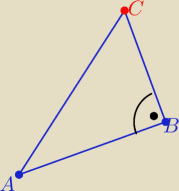
Eta: Proponuję takie rozwiązanie: A(4,3), B(10,5) C(x,2x+3) bo należy do prostej y=2x+3 trójkąt ABC jest prostokątny bo |∡ABC|=90^o−−− z treści → → AB=[6,2] , BC=[x−10,2x−2] i z warunku prostopadłości wektorów: 6(x−10)+2(2x−2)=0 ⇒ x=32/5 to y =..........= 79/5 C(32/5,79/5) ===========

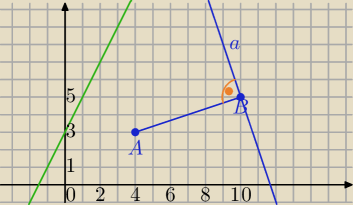
Mila: II sposób AB^→=[6,2] Prosta a⊥AB ma równanie: 6x+2y+C=0 i B∊a⇔6*10+2*5+C=0 C=−70 6x+2y−70=0 /: 2 a: 3x+y−35=0 i y=2x+3

	32		79
x=		i y=
	5		5

C=(6,4;15,8)

asd: Robilem z pitagorasa i dlugosci odcinka i wychodzi inaczej nie wiem dlaczego |CB|²+|BA|²=|AC|²

asd: przy zalozeniu,ze C(x,2x+3)

asd: wychodzi tak samo...nie podnioslem do kwadratu jednej liczby..

Mila: Musiałeś się pomylić w rachunkach, bo wychodzi to samo.