Oblicz najkrótszą i najdłuższą przekątną graniastosłupa Dawid: 1. W graniastosłupie prawidłowym sześciokątnym o krawędzi podstawy długości a krawędź boczna ma długość 2a. Oblicz długość najkrótszej i najdłuższej przekątnej tego graniastosłupa. 2.Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 6√2, a jego wysokość jest równa 4√3. Wyznacz kąt nachylenia przekątnej graniastosłupa do płaszczyzny podstawy. 3.Krawędź boczna graniastosłupa prawidłowego czworokątnego jest trzy razy dłuższa od jego krawędzi podstawy. Oblicz sinus kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy. Proszę o pomoc, wiem że zadania prawdopodobnie są łatwe, ale mam z nimi sporo problemów.

Piotrek: Dołączam się do pytania, umie to ktoś rozwiązać?

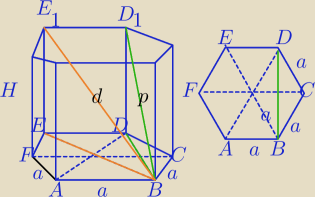
Mila: H=2a 1)

	a√3
|DB|=2*		=a√3
	2

|BE|=2a 2) W ΔBDD₁: p²=(2a)²+(a√3)² p²=4a²+3a²=7a² p=a√7 === 3)W ΔBEE₁: d²=(2a)²+2a)²=8a² d=a√8⇔ d=2√2 a ==========

Mila: Jeśli masz pytania to pisz, wtedy zaczniemy rozw. pozostałe.

Dawid: Pytań nie mam żadnych, ale proszę o pomoc przy innych zdankach

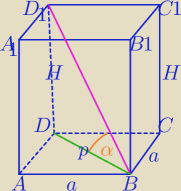
Mila: 2) Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 6√2, a jego wysokość jest równa 4√3. Wyznacz kąt nachylenia przekątnej graniastosłupa do płaszczyzny podstawy. a=6√2 H=4√3

	H
tgα=
	p

p=a√2=6√2*√2 p=12

	4√3
tgα=
	12

	√3
tgα=		⇔
	3

	π
α=
	6

============

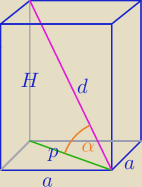
Mila: 3.Krawędź boczna graniastosłupa prawidłowego czworokątnego jest trzy razy dłuższa od jego krawędzi podstawy. Oblicz sinus kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy. H=3a

	H
sinα=
	d

p=a√2 d²=H²+p² d²=(3a)²+(a√2)² d²=9a²+2a²=11a² d=a√11

	3a
sinα=
	a√11

	3
sinα=		⇔
	√11

	3√11
sinα=
	11

===========

Dawid: Serdecznie dziękuję

Mila: Dawid, na drugi raz interesuj się rozwiązaniem wcześniej, staramy się pomagać, nie odrabiamy zadań domowych, bo to żadna pomoc. Masz się nauczyć a nie tylko przepisać.