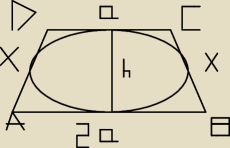
 Oblicz promień okręgu opisanego na trapezie, którego promień okręgu wpisanego ma 2√2, jedna
podstawa jest 2 razy dłuższa od drugiej i wiedząc, że na tym trapezie da się opisać okrąg
Moje obliczenia
r=2√2, więc 2r=4√2=h
Dalej: 3a=2x, więc x=3/2a
Z pitagorasa:
(a/2)2+(4√2)2=(3/2a)2
a=4
Czy promień okręgu opisanego na trapezie nie jest połową przeciwprostokątnej trójkąta ABC,
czyli 4?
Oblicz promień okręgu opisanego na trapezie, którego promień okręgu wpisanego ma 2√2, jedna
podstawa jest 2 razy dłuższa od drugiej i wiedząc, że na tym trapezie da się opisać okrąg
Moje obliczenia
r=2√2, więc 2r=4√2=h
Dalej: 3a=2x, więc x=3/2a
Z pitagorasa:
(a/2)2+(4√2)2=(3/2a)2
a=4
Czy promień okręgu opisanego na trapezie nie jest połową przeciwprostokątnej trójkąta ABC,
czyli 4?
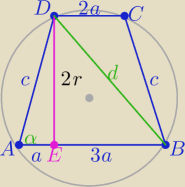 Promień okręgu R opisanego na trapezie jest równy promieniowi okręgu opisanego
na trójkącie ABD
1/ z warunku wpisania okręgu w trapez c+c=6a ⇒ c=3a
to w ΔAED z tw. Pitagorasa : 8a2=4r2 ⇒ ..... a=2
i z tw. Pitagorasa w ΔEBD : d2=...........
Promień okręgu R opisanego na trapezie jest równy promieniowi okręgu opisanego
na trójkącie ABD
1/ z warunku wpisania okręgu w trapez c+c=6a ⇒ c=3a
to w ΔAED z tw. Pitagorasa : 8a2=4r2 ⇒ ..... a=2
i z tw. Pitagorasa w ΔEBD : d2=...........
| 2r | ||
sinα= | =.... | |
| 3a |
| d | ||
2R= | =.......... | |
| sinα |

 sina=4√2/6=2√2/3
62+(4√2)2=|BD|2
|BD|=2√17
2R=2√17*3/2√2=3√34/2
R=3√34/4
Bardzo dziękuję za pomoc Pani Eto i za wskazówkę Pani Blee.
Ja posiedzę pewnie do 4, ale matura dopiero w środę
sina=4√2/6=2√2/3
62+(4√2)2=|BD|2
|BD|=2√17
2R=2√17*3/2√2=3√34/2
R=3√34/4
Bardzo dziękuję za pomoc Pani Eto i za wskazówkę Pani Blee.
Ja posiedzę pewnie do 4, ale matura dopiero w środę  Bardzo dziękuję za pomoc i życzenia powodzenia
Bardzo dziękuję za pomoc i życzenia powodzenia 
 Blee −− to Pan ( wielki Pan
Blee −− to Pan ( wielki Pan 
