Stereometria Aleks: Cześć. Pomoże ktoś? Podstawą ostrosłupa ABCS jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Każda krawędź boczna ostrosłupa ma długość 7. Ściana ASC jest nachylona do płaszczyzny podstawy pod kątem o mierze 45, a ściana BSC pod kątem o mierze 60. Oblicz pole przekroju ostrosłupa ABCS płaszczyzną zawierającą krawędź CS i wysokość ostrosłupa. Jak ostatecznie ma wyglądać rysunek? Z tw. o ostrosłupach wychodzi, że spodek wysokości ma leżeć na przeciwprostokątnej trójkąta w podstawie, ale wtedy tworzą mi się jakieś sprzeczności..

Aleks: ?

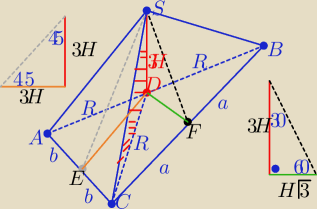
Eta: Spodek wysokości D pokrywa się ześrodkiem okręgu opisanego na podstawie

	1
P(przekroju)=P(ΔCDS)=		*3H*R , R−−dł. promienia okręgu opisanego na podstawie
	2

.......... z tw Pitagorasa w trójkątach CED i CFD R²=(3H)²+b² i R²= (H√3)²+a² i R²+(3H)²=7² i w podstawie 4R²=4a²+4b² ⇒ R²=a²+b² ........................... Odp: P=7√3 =============

Eta: I co Aleks ?

Aleks: Na początku miałem tak samo, ale potem zrezygnowałem. Skoro |DS| jest wysokością, to trójkąt ABS jest prostopadły do podstawy, to czy czasem wtedy trójkąt ASC nie jest prostokątny? Bo jeśli jest to |AS|=|CS|=7, to jest sprzeczność

Wwo: Czym jest ten zielony i pomarańczowy odcinek ?

promując_geogebrę: tutaj to widać https://www.geogebra.org/classic/sd596mej

Wwo: Widać, ale chodzi mi o to czy są to środkowe czy wysokości ? Bo w ostroslupie punkt przecięcia tych prostych wyznacza spodek wysokości.

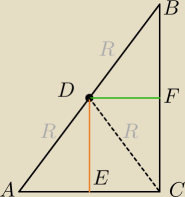
promując_geogebrę: Są to i środkowe i wysokości poprowadzone na boki AC i BC.

promując_geogebrę: Odpowiednio w trójkątach ΔADC i ΔBDC.

Wwo: Ale czy wysokością na bok AC nie jest BC i na odwrót?

promując_geogebrę: Tak, dlatego ta uwaga, że są to środkowe i wysokości poprowadzone na boki AC i BC w trójkątach ΔADC i ΔBDC.

Wwo: Rozumiem, ale w takim razie jak przeciętny człowiek może wpaść na pomysł by poprowadzić środkową na bok AB i z powstałych dwóch trójkątów również poprowadzić środkowe ? Bez których notabene nie zrobiloby się tego zadania.

ite: Te środkowe to skutek wcześniejszych ustaleń. Najpierw zauważamy, że każda krawędź boczna ostrosłupa ma długość 7. ↓ Ściany boczne są trójkątami równoramiennymi. Spodek wysokości D pokrywa się ze środkiem okręgu opisanego na podstawie (to co napisała Eta 23:32). ↓ Narysowanie ΔADC i ΔBDC (rzuty ścian bocznych) i zauważenie, że też są trójkątami równoramiennymi o bokach R, zaznaczenie w nich tego zielonego i pomarańczowego odcinka.