Zadanie z Planimetrii 123: Niech ABCD będzie kwadratem. Zakreślono okrąg o środku B i promieniu |AB|. Następnie poprowadzono okrąg leżący wewnątrz kwadratu ABCD, styczny do boków AD i DC i zewnętrznie styczny do okręgu o środku B. Wyznacz promień małego okręgu. Proszę o wskazówki, co w jakiej kolejności powinienem liczyć. Z góry dziękuję.

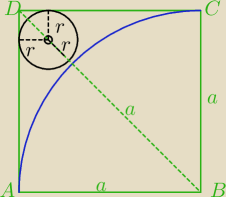
iteRacj@: AD − przekątna kwadratu AD − jest sumą boku kwadratu, jego promienia i przekątnej kwadratu o boku r

iteRacj@: * poprawka BD

123: Rozumiem |BD|=a+r+r√2 Tylko wynik musi wyjść: 3−2√2

iteRacj@: czy |AB|=1?

123: Przepraszam, |AB|(3−2√2)

123: Jeszcze dopytam, jak uzależnić r od a? Coś w stylu: a=x+r i podstawianie?

iteRacj@: taki właśnie jest wynik: |AB|=a √2a−a=r+√2r a(√2−1)=r(√2+1)

	√2−1
r=|AB|*
	√2+1

teraz tylko usuń niewymierność z mianownika

iteRacj@: r jest powiązane z a w równaniu √2a=a+r+√2r

123: Rozumiem, bardzo Panu dziękuję: √2−1/√2+1*√2−1/√2−1=(√2−1)²

iteRacj@: dobrze, że wszystko jest jasne (a panem nie jestem )

123: Przepraszam, to jeszcze raz Pani dziękuję

iteRacj@: