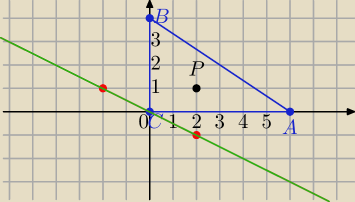
Udowodnienie że A,C,B leza na jednej prostej shirori: Punkt P leży wewnątrz trójkąta o wierzchołkach A=(6,0), B=(0,4), C=(0,0). Oznaczmy przez PAC obraz punktu P w symetrii osiowej względem prostej AC, a przez PBC obraz punktu P w symetrii osiowej względem prostej BC. Uzasadnij, że punkty PAC, C i PBC leżą na jednej prostej. Zrobilam rysunek, ale jak to udowodnić? W sensie C jest zawsze 0,0 ; A to −6;0 ; B 0,−4 leza na tej samej, ale czy rysunek wystarczy?

iteRacj@: Nie, rysunek nie jest tu dowodem. Te trzy punkty PAC, C i PBC są współliniowe, jeśli odlegość dwóch skrajnych (PAC i PBC) jest równa sumie odległości sąsiednich (od PAC do C i od C do PBC). Ustal współrzędne obrazów punktu B w obu symetriach osiowych. Oblicz odległości między punktami PAC, C i PBC.

Mila: P=(p,q) P₁=P_ac=(p,−q) P₂=P_bc=(−p,q) C=(0,0) Prosta przechodząca przez C(0,0) ma wzór y=m*x Sprawdzamy czy punty P₁,P₂,C leżą na jednej prostej

	−q
−q=m*p⇔m=
	p

	q
Prosta CP1: y=(−		)*x
	p

	q
y=(−		)*(−p)=q⇔P2 lezy na prostej CP1
	p

shirori: Super dziekuje! Tak cos czulam ze za latwo.. xd

Mila: