matura
Kacper:
No maturka tuż tuż, to może i zadanka?
1. Oblicz objętość ostrosłupa prawidłowego czworokątnego o wysokości długości h i kącie o
mierze 2α między sąsiednimi ścianami bocznymi ostrosłupa.
| | |AB| | | 2+√2−√3 | |
2. Kąt ostry BAD równoległoboku ABCD ma miarę 30o, oraz |
| = |
| . |
| | |AD| | | 2 | |
Dwusieczna kąta wypukłego ADC przecina bok AB w punkcie E. Uzasadnij, że w czworokąt
EBCD można wpisać okrąg.
6 maj 16:22
Mila:
Witaj
Kacper, co słychać u Ciebie, rzadko się udzielasz na forum

6 maj 19:26
Benny: Jakiś dziwny wynik dostałem w tym 1.
| | 4h3sin4α | |
V= |
| |
| | 3[1+2sin2α−sin4α] | |
6 maj 19:52
Krzysiekmatura: Jak się oblicza kąt między ścianami

6 maj 19:57
PW: Najpierw "jak się rysuje kąt między ściamami", czyli jaka jest definicja.
6 maj 20:00
Benny: Kacper masz wynik do tego zadania?
6 maj 20:02
Szczeniak: Rysujesz wysokości ścian bocznych będącymi przystającymi trójkątami równoramiennymi, padające
na wspólną krawędź sąsiednich ścian bocznych
6 maj 20:53
Mila:
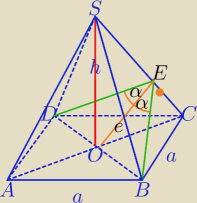
1)
Oblicz objętość ostrosłupa prawidłowego czworokątnego o wysokości długości h
i kącie o mierze 2α między sąsiednimi ścianami bocznymi ostrosłupa.
Rozw.
|AC|=2d
|OC|=d=|OB|,
DE⊥SC, EB⊥SC, OE⊥SC,
| | d | |
1) W ΔEOB: tgα= |
| ⇔d=e*tgα⇔ (*) e=d*ctgα |
| | e | |
|EC|
2=d
2−e
2=d
2−d
2ctg
2α⇔|EC|=d*
√1−ctg2α
2)
ΔSEO∼ΔCEO⇔
| e | | EC | | e | | d*√1−ctg2α | |
| = |
| ⇔ |
| = |
| ⇔ (**) e=h*√1−ctg2α |
| h | | OC | | h | | d | |
3) Z(*) i (**)
| | 1 | | 1 | | 4h2*(1−ctg2α) | |
PABCD= |
| (2d)2= |
| * |
| =2h2*(tg2α−1) |
| | 2 | | 2 | | ctg2α | |
4)
==============
6 maj 21:00
Eta:
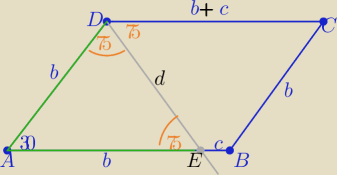
1/ rysunek zgodny z treścią zadania
z warunku wpisania okręgu w czworokąt
należy wykazać,że d+b=c+b+c czyli wykazać,że
d=2c
ΔAED równoramienny −−− dlaczego?
to |AE|=|AD|=b
z tw. cosinusów w ΔAED: .......... d
2=b
2(2−
√3)
to
d= b*√2−√3
| | b+c | | √2−√3 | |
z treści zadania: |
| = |
| ⇒ ........... 2c=b√2−√3 |
| | b | | 2 | |
zatem d=2c
c.n.w
6 maj 21:27
Kacper:
Cześć
Mila 
sporo się zmienia w życiu i czasu brak żeby zaglądać na forum.
Przy okazji wynik poprawny

Pozmieniało się widzę, skoro zadanka liczą już tylko osoby, które nie są maturzystami

6 maj 21:34
Saizou :
To ja też dorzucę swoje 3 grosze. Zadanie choć nie jest maturalne, ale jest ciekawe.
Poczta na Wyspie Zagadkowej wprowadziła pewne ograniczenia związane z przesyłkami i nie
przyjmuje do wysyłki paczek dłuższych niż 1 metr; firmy kurierskie akurat strajkują. Pan
Fletowski chce przesłać pilnie swój cenny flet o długości 1 metr i 30 centymetrów. Czy
istnieje możliwość przesłania fletu?
6 maj 21:57
Krzysiekmatura: nie
6 maj 22:18
KWR: Zalezy jaki flet
jesli poprzeczny to np firmy YAMAHA jesdt rozkladany wiec istnieje
6 maj 22:21
Jack: na podstawie to chyba zadania typu
x2 + 4x − 5 > 0
6 maj 22:24
inż. Hugo:

Powodzenia jutro
6 maj 22:40
inż. Hugo: @Jacek
16+20 = 36 delta
x1 = (−4 −6 )/2
x2 = (−4+6)/2

Z moich czasów PR
Ciąg geometryczny (an) ma 100 wyrazów i są one liczbami dodatnimi.
Suma wszystkich wyrazów o numerach nieparzystych jest
sto razy większa od sumy wszystkich wyrazów numerach parzystych
oraz loga
1 + loga2 + loga
3 + .... + loga
100 = 100, oblicz a
1
6 maj 22:50
Spongebob: E, to autoportret?
6 maj 22:55
Metis: 
7 maj 01:43
Hugo: Hugo byl tak zesresowany ze mu wlosy deba stanely

7 maj 08:37
SuSu:
Mila
| | 2 | | 1 | |
Mi wyszła objętość V= |
| h3(tg |
| α−1) |
| | 3 | | 2 | |
A to pewnie dlatego ze mam kąt α miedzy sąsiednimi ściamami bocznymi
5 sie 16:46


 1)
Oblicz objętość ostrosłupa prawidłowego czworokątnego o wysokości długości h
i kącie o mierze 2α między sąsiednimi ścianami bocznymi ostrosłupa.
Rozw.
|AC|=2d
|OC|=d=|OB|,
DE⊥SC, EB⊥SC, OE⊥SC,
1)
Oblicz objętość ostrosłupa prawidłowego czworokątnego o wysokości długości h
i kącie o mierze 2α między sąsiednimi ścianami bocznymi ostrosłupa.
Rozw.
|AC|=2d
|OC|=d=|OB|,
DE⊥SC, EB⊥SC, OE⊥SC,
 1/ rysunek zgodny z treścią zadania
z warunku wpisania okręgu w czworokąt
należy wykazać,że d+b=c+b+c czyli wykazać,że d=2c
ΔAED równoramienny −−− dlaczego?
to |AE|=|AD|=b
z tw. cosinusów w ΔAED: .......... d2=b2(2−√3)
to d= b*√2−√3
1/ rysunek zgodny z treścią zadania
z warunku wpisania okręgu w czworokąt
należy wykazać,że d+b=c+b+c czyli wykazać,że d=2c
ΔAED równoramienny −−− dlaczego?
to |AE|=|AD|=b
z tw. cosinusów w ΔAED: .......... d2=b2(2−√3)
to d= b*√2−√3
 sporo się zmienia w życiu i czasu brak żeby zaglądać na forum.
Przy okazji wynik poprawny
sporo się zmienia w życiu i czasu brak żeby zaglądać na forum.
Przy okazji wynik poprawny  Pozmieniało się widzę, skoro zadanka liczą już tylko osoby, które nie są maturzystami
Pozmieniało się widzę, skoro zadanka liczą już tylko osoby, które nie są maturzystami 
 Powodzenia jutro
Powodzenia jutro
 Z moich czasów PR
Ciąg geometryczny (an) ma 100 wyrazów i są one liczbami dodatnimi.
Suma wszystkich wyrazów o numerach nieparzystych jest
sto razy większa od sumy wszystkich wyrazów numerach parzystych
oraz loga1 + loga2 + loga3 + .... + loga100 = 100, oblicz a1
Z moich czasów PR
Ciąg geometryczny (an) ma 100 wyrazów i są one liczbami dodatnimi.
Suma wszystkich wyrazów o numerach nieparzystych jest
sto razy większa od sumy wszystkich wyrazów numerach parzystych
oraz loga1 + loga2 + loga3 + .... + loga100 = 100, oblicz a1

