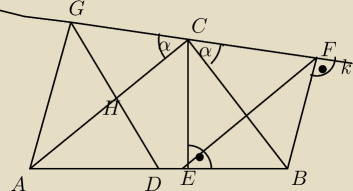
Geometria płaska, problem polo: DH || CB i |AD|=|DB| Dlaczego z tych dwóch powyższych warunków wynika, że |AH|=|HC|?

polo: bump

iteRacj@: wpisz treść zadania, bo z rysunku niewiele wiadomo

polo: Dany jest trójkąt ABC, którego boki spełniają nierówność |AB|>|AC|>|BC|. Przez wierzchołek C trójkąta ABC przeprowadzoną prostą k, która tworzy z bokami BC i AC takie same kąty. Na prostej AB i k wybrano odpowiednio po dwa punkty D i E oraz F i G takie, że |AD|=|BD|, CE⊥AB, BF⊥k, DG || BC. Uzasadnij, że na czworokącie DEFG można opisać okrąg (to zrobiłem) oraz, że AG⊥k.

iteRacj@: Dlaczego z tych dwóch powyższych warunków wynika, że |AH|=|HC|?

	1
z podobieństwa ΔABC i ΔAHD (kbk) wynika, że |AH|=		|AC|
	2

a z tego już |AH|=|HC|

polo: @iteRacj@ Wielkie dzięki