... Agata: Zbadaj prawdziwość następujących zdań: a) Jeśli funkcja f0,1]−−>R ma własność Darboux, to jest ciągła; b) Każda funkcja f:(0,1)−−>R osiąga kresy zbioru swoich wartości. Udowodnij lub podaj kontrprzykład.

Agata: a) f : [0,1] −−−> R

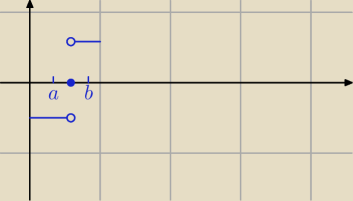
PW: Kontrprzykład do a) Wykres unkcji składa się z dwóch niebieskich odcinków i niebieskiej kropki. f(a)<0 i f(b)>0, w przedziale (a, b) istnieje miejsce zerowe, ale funkcja nie jest ciągła.

Adamm: to nie jest własność Darboux PW

Adamm: b) nie jest prawdą nawet dla funkcji ciągłych

Blee: Adamm ma rację PW ... ta funkcja nie ma własności Darboux −−− przeciwobraz nie zawiera całego przedziału <f(a) , f(b)> Ale już:

	⎧	sin(1/(x−0.5)) dla x≠0.5
f(x) =	⎩	0 dla x=0.5

Blee:

	1		1
b) niech f(x) =		+
	x		x−1

PW: Licho weźmie, pamięć zawodzi, a nie chciało się sprawdzić. Przepraszam.