monotonicznosc Szczeniak: Funkcja określona jest wzorem f(x)=x²+mx+1 dla x<2 oraz −3x−9 dla x≥2. Znajdź te wartości parametru m, dla których funkcja f jest malejąca.

Szczeniak: Jakieś wskazówki? W przedziale (−∞,2) jest parabola o ramionach skierowanych do góry to jak funkcja ma być malejąca

the foxi: funkcja określona na przedziale x≥2 jest już malejąca więc musimy tak dobrać m, żeby i ta po lewej była malejąca zauważ, że współczynnik przy x² jest a=1, czyli parabola jest "uśmiechnięta". co to znaczy? że do swojego wierzchołka maleje, potem rośnie. czyli dopóki wierzchołek będzie poza przedziałem x<2, funkcja będzie malejąca

	b
współrzędna iksowa wierzchołka dana jest wzorem xw=−
	2a

	m
xw=−
	2

pamiętasz jaki warunek musi spełniać wierzchołek? być poza przedziałem x<2, czyli po prostu znajdować się w x=2 albo większym

	m
−		≥2
	2

−m≥4 m≤4

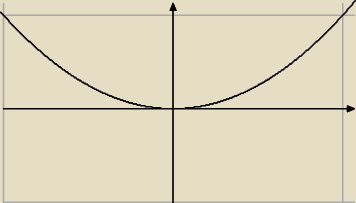
the foxi: no tak, skoro ramiona są skierowane do góry, to po lewej stronie wierzchołka funkcja maleje − popatrz sam

Basia: y=−3x−9 jest zawsze malejąca więc można się nią dalej nie zajmować istotne jest tylko to, że dla x=2 y=−15

	−m
y=x2+mx+1 musi być malejąca w przedziale (−∞;2) a to jest prawdą ⇔ xw=		≥2 ⇔
	2

−m≥4 ⇔ m≤ −4 ponadto musi być spełniony warunek: lim_x→2(x²+mx+1)≥ −15 4+2m+1≥ −15 2m ≥ −20 m≥ −10 Odp: m∊<−10;−4> Uwaga dodatkowa: dla m=−10 funkcja będzie ciągła w p−cie x=2 dla m∊(−10;−4> warunki zadania bedą spełnone, ale funkcja nie będzie ciągła w p−cie x=2

the foxi: faktycznie, ten drugi warunek też jest bardzo ważny

Szczeniak: Pierwszy warunek zrozumiałem, moglibyście rozjaśnić sprawę z tą granicą? Bardzo proszę

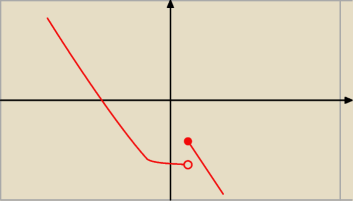
the foxi: wyobraź sobie, że granica przy x−>2 z lewej strony jest równa np. −20 funkcja maleje, maleje do 2 i nagle przeskok wartości w górę do −15 i znowu maleje rysunek przykładowy widzisz ten mały przeskok do góry?

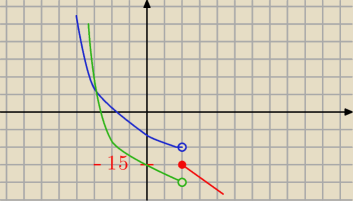
Basia: gdyby to ramię paraboli "zeszło" poniżej −15 (patrz zielone) funkcja nie byłaby malejąca w całej dziedzinie byłaby tylko malejąca przedziałami

the foxi: haha i znowu Pani nieco lepiej wyjaśniła

Szczeniak: Ok, czyli żeby nie było tego przeskoku tzn funkcja nie rosła na tym malym odcinku to granica przy x−>2 z lewej strony musi być równa f(2) czyli −15

Basia: musi być większa lub równa −15

Szczeniak: No tak. Dzięki króle złote