Funkcja z parametrem adastach4: Dla jakich wartości parametru k funkcja f określona wzorem

	⎧	(2−k)x−3k dla x∊(−∞; −2)
f(x)=	⎩	−2 x2 +(k−10)x+1−7k dla x∊<−2; +∞)	przyjmuje tylko

wartości ujemne?

Basia: nie może być 2−k<0 bo wtedy lim_x→−∞ f(x) = +∞ czyli musi być 2−k≥0 ⇔ k≤2 dla k=2 masz

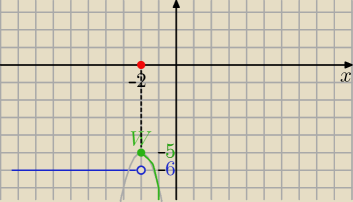
	⎧	−6 dla x∊(−∞;−2)
f(x) =	⎩	−2x2−8x−13 dla x∊<−2;+∞)

Δ−64−4*(−2)*(−13)<0 ramiona w dół czyli na pewno mamy tylko wartości ujemne dla k<2

	3k
musi być x0 =		≤−2 (to łatwo przeliczyć)
	2−k

i (Δ<0 (to jeszcze jakoś pójdzie) lub Δ=0 i x₀<−2 (to też jakoś pójdzie) lub Δ>0 i x₁,x₂<−2) możliwe, że się gdzieś pomyliłam bo jakieś koszmarne obliczenia mi z tego wychodzą

Eta: Hej Basia to może tak: f₁(x)=(2−k)x−3k <0 dla x< −2 funkcja liniowa spełnia ten warunek gdy: 2−k≥0 i (2−k)*(−2)−3k≤−2 ( bo dla krańcowej z lewej strony uwzględniam miejsce zerowe x= −2 zatem k≤2 i k≥ −4 ⇒ k∊<−4,2> ========= dla f₂(x)=−2x²+(k−10)x+1−7k <0 −−− parabola ramionami w dół należy ustalić gdzie znajduje się wierzchołek paraboli po prawej czy po lewej stronie x= −2

	k−10
xw=		≥ −2 ⇒ k ≥2 i dla f1(x) k∊<−4,2> więc dla k=2
	4

odcięta wierzchołka dla k=2 x_w= −2 to f₂(x)= −2x²−8x−13 y_w= f(−2)= −5 W(−2, −5) więc f₂(x) <0 dla k=2 i x≥ −2 Zatem warunki zadania spełnia tylko k=2 f₁(x)= −6 dla x<−2 f₂(x)= −2x²−8x−13 dla x≥ −2 Ciekawe zadanko