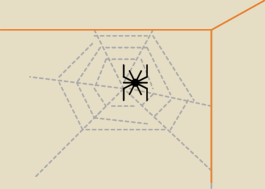
Matura 2018 - zadania Saizou : Ktoś gdzieś w poście wrzucił propozycję zadań maturalnych. Tak więc osoba, która rozwiąże zadanie, wrzuca kolejne itd. Fajnie abyście numerowali zadania, aby było czytelniej. Piszcie też, które zadanie rozwiązujecie, aby było łatwiej sprawdzać (przy okazji możecie wrzucać rozwiązania już rozwiązanych problemów, ale w inny sposób) Zad 1 Pająk siedzi na środku krawędzi ściany pokoju ( w kształcie sześcianu) i spostrzega w najdalej oddalonym kącie muchę. Posuwa się ku niej po najkrótszej drodze ( po linii prostej). Jaka jest wartość tej drogi do muchy ?

Blee: Zadanie z pająkiem Jak ktoś potrafi pomyśleć chwileczkę, to zadanie na 2 minuty (wliczając to wstępne myślenie)

iteRacj@:

Saizou : Owszem, ale nie wszystko na maturze musi być poziom hard

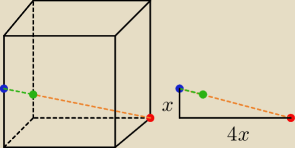
Blee: No to w takim razie rozwiązanie trójkąt prostokątny o bokach x i 4x ; gdzie x = połowa krawędzi

	√5
D = √5x =		a ; gdzie a −−− długość krawędzi
	2

Saizou : źle

Blee: Zad 2 Dla jakich parametrów k∊R funkcja

	x3 − kx2 + 3
f(x) =
	kx − 1

będzie nieparzysta

Franklin p_p: Zad1 x+x√2 droga pająka

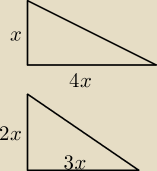
Blee: reflektuję się −−− bo nie ma to jak nie podnieść do kwadratu w tw. Pitagorasa musimy rozpatrzyć dwa trójkąty prostokątne: 1) idzie po dwóch ścianach bocznych 2) idzie po ścianie bocznej i podłodze d₁ = √17x d₂ = √15x

	√15
Odp.: D =		a
	2

Blee: tfu ... (znowu) d₂ = √13x idę dalej pić, bo myślenie mi nie wychodzi

Saizou :

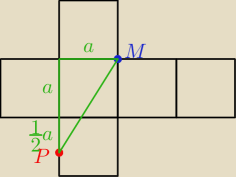
	√13
Odpowiedź to		a, gdzie a to długość krawędzi sześcianu.
	2

Można to było też drogę pająka rozrysować na siatce sześcianu z tw. Pitagorasa mamy

	9		13
|PM|2=		a2+a2=		a2
	4		2

	√13
|PM|=		a
	2

Franklin p_p: W zadaniu 2 kx≠1 k=0 , ponieważ dziedzina funkcji musi być symetryczna względem zera?

Luki: Czy zadanie 2 jest takie proste?

Saizou : to jakie jest wg Ciebie rozwiązanie?

Luki: No wg mnie ok