Równania trygonometryczne Kweszczon: Hej, sformułowanie odpowiedzi do zadania stanowi dla mnie kłopot. Mogę prosić Was o wyjaśnienie? ,,Dla jakich wartości α∊[0; 2π] równanie x² + 2xcosα + 1 = cos²α nie ma pierwiastków rzeczywistych"? x² + 2xcosα + 1 − cos²α = 0 4cos²α − 4 + 4cos²α = 0 cos²α = ¹₂ cosα = − ^√2₂ ∨ cosα = ^√2₂ Odpowiedż w zbiorze zadań: α∊(^π₄; ^3π₄)∪(^5π₄; ^7π₄) Dlaczego nie α∊ℛ\{^√2₂} ∨ α∊ℛ\{^√2₂}?

Kweszczon: Przepraszam, poprawiam swoją odpowiedź: α∊ℛ\{^π₄}∨α∊ℛ\{−^π₄}

iteRacj@: równanie kwadratowe nie ma rozwiązań rzeczywistych ⇔ Δ<0 u Ciebie równa zero

Kweszczon: Czy w podanym przez Ciebie przypadku x∊ℛ? Spójrz na parabolę. Tylko nie wyznaczasz miejsca zerowego.

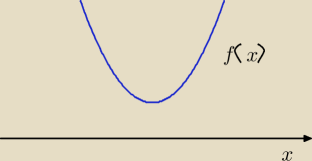
iteRacj@: x∊ℛ, cos α to parametr, α ma spełnić warunki α∊[0; 2π] szukamy wartości parametru, dla których wykres funkcji f(x) =x²+2xcos α+1−cos²α czyli parabola jest położona tak jak na rysunku wtedy wyjściowe równanie kwadratowe nie ma rozwiązań rzeczywistych

	1
a to zachodzi gdy Δ<0 czyli cos2α<		, a=1 czyli a>0
	2

Kweszczon: Przypomnielibyście zagadnienie, typ zadań, w których ujemna delta oznacza × należy do R?

Adamm: Nierówności kwadratowe