 Cześć, pomoże ktoś?
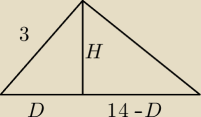
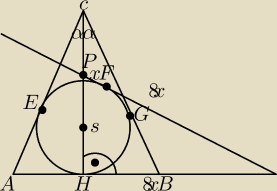
W trójkąt równoramienny ABC wpisano okrąg o środku w punkcie S. Punkty E,G,H to punkty
styczności
tego okręgu z trójkątem. Poprowadzono styczną do okręgu w punkcie F, która przecięła dwusieczną
kąta zawartego między ramionami trójkąta w punkcie P, ramię AC w punkcie Q oraz przedłużenie
podstawy AB w punkcie D. Wiedząc, że stosunek długości odcinka |FD| do |PF| jest równo 8:1 oraz
|FG|=6, |EF|=6√17, |EG|=28:
Cześć, pomoże ktoś?
W trójkąt równoramienny ABC wpisano okrąg o środku w punkcie S. Punkty E,G,H to punkty
styczności
tego okręgu z trójkątem. Poprowadzono styczną do okręgu w punkcie F, która przecięła dwusieczną
kąta zawartego między ramionami trójkąta w punkcie P, ramię AC w punkcie Q oraz przedłużenie
podstawy AB w punkcie D. Wiedząc, że stosunek długości odcinka |FD| do |PF| jest równo 8:1 oraz
|FG|=6, |EF|=6√17, |EG|=28:
| |AB| | 2|CH| | |||
a)wykaże, że prawdziwa jest równość | = | |||
| |HP| | |FD| |
| |AB| | 2|CH| | |AH| | |HP| | ||||
= | ⇔ | = | ⇔ | ||||
| |HP| | |FD| | |CH| | |HD| |
| 8 | ||
wiemy że cos∡PDH= | pokażemy że cos∡EOS wynosi tyle samo | |
| 9 |
| 13 | ||
d= | dalej | |
| 7 |
| 13 | ||
32− ( | )2=h2 | |
| 7 |
| 4√17 | ||
h= | ||
| 7 |
| 4√17 | ||
PΔ=0,5* | *14=4√17 | |
| 7 |
| abc | ||
teraz ze wzoru R= | R=0,5|ES|=7,875 więc |ES|=15,75 | |
| 4P |
| |EO| | 14 | 8 | ||||
wracając do cos∡EOS= | = | = | ||||
| |ES| | 15,75 | 9 |
| 9+√17 | ||
i wyszło mi ( | )2 bardzo możliwe że źle bo nieprzyjemne liczby. | |
| 17 |