Funkcja wymierna oraz pochodne Adam:

	ax+1+ba
Wiadomo ,że funkcja f(x) = |		| jest rosnąca w przedziałach ( − ∞ , −2) i <−1,
	x+b

+∞) oraz malejąca w przedziale (−2 , −1>. Zatem: a) a = 1 b) a = −1 c) a = 2 d) a = −2 Czy mógłby ktoś wytłumaczyć jak zrobić to zadanie?

ReMi: To jest zadanie pewnie maturalne, jest to zadanie zamknięte − jeśli ktoś myśli o dużych % na maturze to musi się śpieszyć, bo czasu jest mało, podstaw szybko te wartości a zobacz jak będą wyglądać funkcje O wiele szybciej to idzie niż liczenie na piechotę

iteRacj@:

	ax+1+ba
f(x)=|		| D=R\b
	x+b

	a(x+b)+1		1
f(x)=|		|=|a+		|
	x+b		x+b

iteRacj@:

iteRacj@: rysunek pomoże zrozumieć o co chodzi w rozwiązaniu, ale sposób ReMi szybszy

La gringa: Wybaczcie że podbijam, ale wgl nie rozumiem jak rozwiązywać tego typu zadania Zrobiłam tak jak Remi czyli podstawiłam za a wartości z podpunktów do wzoru iteRacj@ No i otrzymałam:

	1
|1+		|
	x+b

	1
|−1+		|
	x+b

	1
|2+		|
	x+b

	1
|−2+		|
	x+b

Ale nie wiem teraz, z której strony to ugryźć/ narysować wykres, zrozumieć Stres przedmaturalny daje się we wznaki

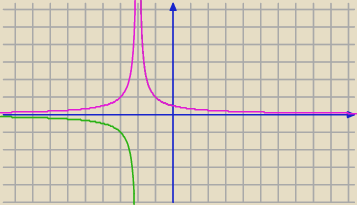
iteRacj@: Przekształcenie wzoru funkcji homograficznej do podanej przez mnie postaci ułatwia określenie jej asymptot i umożliwia szybkie naszkicowanie.

	a(x+b)+1		1
g(x)=		=a+		, D=R\{−b}
	x+b		x+b

asyptota pionowa x=−b, asymptota pozioma to y=a Skoro dziedzinę funkcji tworzą przedziały (−∞;−2) i <−1;∞) oraz (−2 , −1> to widać, że −b=−2 .

	1
Zatem g(x)=a+		i asyptota pionowa ma wzór x=−2.
	x+2

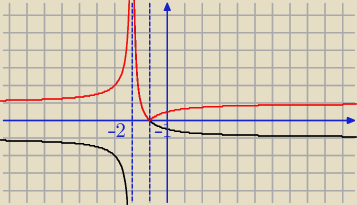
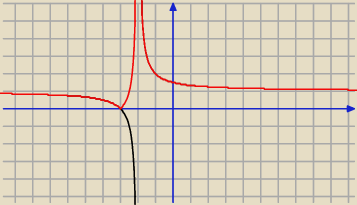
Teraz trzeba się zastanowić, w jakiej sytuacji funkcja f(x) czyli ta z wartością bezwzględną będzie mieć trzy przedziały monotoniczności. Przy asymptocie y=0 przedziały będą dwa. Rysunek powyżej. Gdy a<0 przedziały będą trzy (f. rośnie, maleje, rośnie). Rysunek z 11:24. Gdy a>0 przedziały będą trzy (f.maleje, rośnie, maleje). Rysunek poniżej. W tym zadaniu po naszkicowaniu wykresy g(x) a potem f(x) trzeba sprawdzić dla jakiego a przedziały monotoniczności będą takie jak podane w zadaniu.

iteRacj@:

iteRacj@: @La gringa możesz też tylko podstawić, tak jak radzi ReMi: 1. najpierw zauważasz, że do dziedziny nie należy −2, więc −b=−2

	1		1
g(x)=a+		=a+
	x+b		x+2

2. zauważasz, że miejscem zerowym funkcji jest (−1) czyli g(−1)=0

	1
0=a+		stąd a=−1
	−1+2

	1
3. szkicujesz wykres f(x)=|−1+		| dla sprawdzenia wyniku i terminado
	x+2