Geometria analityczna

Geometria analityczna UczącySię: Promień światła biegnie po prostej o równaniu x−2y+5=0.Po dojściu do prostej 3x−2y +7=0promień odbija się od niej. Napisać równanie prostej na której leży odbity promień. Wielu rzeczy spróbowałem i nie wyszło. Chciałem z odległością punktu od prostej ale nie udało mi się, proszę o wskazówkę !

2 maj 01:24

Adamm: ax+by+c=0 (1, −2)•(3, −2)=7=√5*√13*cosα (a, b)•(3, −2)=3a−2b=−√5*√13*cosα 3a−2b+7=0 np. a=1, b=5 x−2y+5=0 3x−2y+7=0 x=−1, y=2 c=−9 x+5y−9=0

2 maj 01:37

UczącySię: Odpowiedź mam inną

I też nie wiem dokładnie co robisz tutaj

2 maj 01:43

Mila: Napisz tę odpowiedź. Liczę.

2 maj 18:56

Tadeusz: punkt przecięcia ubu prostych a potem ...

2 maj 19:01

Mila:

	1		5
k: x−2y+5=0⇔y=		x+
	2		2

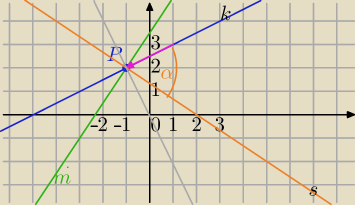
m: 3x−2y +7=0 1) Punkt przecięcia: P=(−1,2) 2) s⊥m, prostopadła do m, P∊s

	−2		4
y=		x+
	3		3

3) tangens kąta między prostymi: k i s

1/2+2/3

tgα=|

 1 −2 
1+
*
|
 2 3 

	7
tgα=
	4

	7
4) tangens kąta między prostymi=		: k i p ( promieniem)
	4

p: y=ax+b

7

 2 
a+
 3 

=|

|

4

 −2 
1+a*
 3 

Licz a i b , po kolacji ja dokończę.

2 maj 19:43

Mila:

	29
a=		, P∊p
	2

	29		33
y=		x +
	2		2

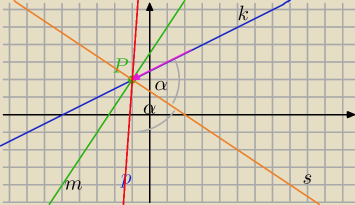
2 maj 20:37

Mila: Może spojrzy tu Eta, ma inny sposób.

2 maj 23:25

UczącySię: Jestem. Bardzo dziękuję za rozwiązanie, nigdy bym nie wpadł, że to tak wygląda ... emotka

3 maj 00:13

Adamm: Próbowałem pójść na łatwiznę, i znowu zastosowałem iloczyn skalarny

3 maj 00:16

Adamm: To nie był zły pomysł, ale można byłoby więcej nad tym pomyśleć

3 maj 00:19

Pytający: Adamm, kąt jest taki sam, zatem powinno być (chociaż pewnie już to zauważyłeś): (1, −2)•(3, −2)=7=√5*√13*cosα (a, b)•(3, −2)=3a−2b=√a²+b²*√13*cosα ⋀ (a,b)≠(1,−2) Stąd: a=29/13, b=−2/13 ⇒ c=33/13 (dla x=−1, y=2) I wychodzi to samo: 29x−2y+33=0

3 maj 01:44