Logarytmiczne nierówności trygonometryczne
Kweszczon: Mogę prosić o wskazówkę do zadania?
| | 1 | | 1 | |
log |
| |sinx| < log |
| |cosx| |
| | 2 | | 2 | |
| 1 | |
| jako podstawa logarytmu |
| 2 | |
1 maj 21:49
aniabb: |sinx|>|cosx|
1 maj 21:52
Lech: Po opuszczeniu log otrzymujesz : | sin x | > | cos x|
Wykonaj wykres tych funkcji i na tej podstawie okreslisz przedzialy
x =( π/4 + kπ , 3π/4 + kπ )
1 maj 21:55
Kweszczon: Albo pora na dobranoc, albo naprawdę nie widzę sposobu opuszczenia logarytmu...
1 maj 22:05
PW: Masz rację, nie ma takiej operacji matematycznej

Można skorzystać z monotoniczności
funkcji logarytmicznej o podstawie mniejszej od 1.
1 maj 22:11
Mila:
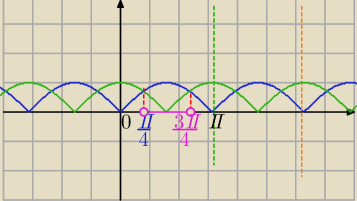
|sinx|>|cosx|
T=π
wynik : Jak napisał kolega
Lech
1 maj 23:21
 Można skorzystać z monotoniczności
funkcji logarytmicznej o podstawie mniejszej od 1.
Można skorzystać z monotoniczności
funkcji logarytmicznej o podstawie mniejszej od 1.
 |sinx|>|cosx|
T=π
wynik : Jak napisał kolega Lech
|sinx|>|cosx|
T=π
wynik : Jak napisał kolega Lech