Logarytmiczne nierówności trygonometryczne Kweszczon: Cześć, plączę się z poniższym przykładem:

	1		3		1		2   3   3
3log		(sin2x −		sinx +		) <
	2		2		2		√3

	1
Po prawej: logarytm o podstawie		, w nawiasie liczba logarytmowa.
	2

	3		1		1		1
Po zabawie otrzymuję 0 = sin2x −		sinx +		−
	2		2		2		6

	1		1		1
Ostatnia grupa:		odjąć		podniesiona do potęgi
	2		2		6

Męcząc się z pierwiastkiem z delty, podejrzewam, że popełniam błąd bądź pomijam oczywiste rozwiązanie.

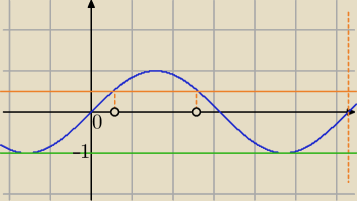Mila: 1) Dziedzina:

	3		1
sin2x−		sinx+		>0
	2		2

sinx=t, |t|≤1

	1
−1<sinx<
	2

Odczytujesz z wykresu 2) Dalej Nierówność nieciekawa, może coś źle przepisałeś.

	3		1		1
log12(sin2x−		sinx+		)<
	2		2		6