NIerównośći trygonometryczne Kweszczon: Hej! Trygonometrii nigdy zbyt wiele: cos4x + 2cos²x < 1 cos4x + 2cos²x − 1 < 0 cos4x + cos2x < 0 Z wzoru na sumę funkcji trygonometrycznych: 2cos3xcosx < 0 Rozważam dwa przypadki: 1) cos3x > 0 cosx < 0

	π		π
Otrzymuję		> x >
	2		6

	π		π		3π		11π
Zapisuję x ∊ (		;		)∪(		;		)
	6		2		2		6

2) cos3x <0 cosx < 0 ∅

	π		5π		7π		3π
Dlaczego w odpowiedziach występuje dodatkowo (		;		)∪(		;		)?
	2		6		6		2

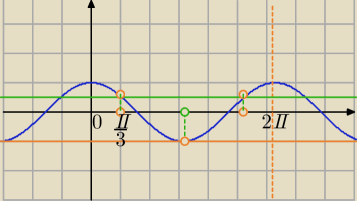
Analizując wykres, dostrzegam związek między zbiorami, jednak nie potrafię uzasadnić na podstawie obliczeń.

Lech: cos 3x * cos x < 0 ⇔ ( cos 3x < 0 i cos x > 0 ) lub ( cos 3x > 0 i cos x < 0 )

Kweszczon: Przepraszam, widzę, że nieprawidłowo zapisałem 2) Wciąż nie rozumiem odpowiedzi w zbiorze...

Mila: Czy masz podać rozwiązania w przedziale <0,2π> ?

Kweszczon: Tak!

Mila: cos4x + cos2x < 0⇔ 2cos²(2x)+cos(2x)−1<0 cos(2x)=t, |t|≤1 2t²+t−1<0 Δ=9

	1
t=−1 lub t=
	2

	1
t∊(−1,		)⇔
	2

	1
−1<cos(2x)<
	2

π		5π
	+2kπ<2x<π+2kπ lub π+2kπ<2x<		+2kπ /:2
3		3

π		π		π		5π
	+kπ<x<		+kπ lub		+kπ<x<		+kπ
6		2		2		6

k=0

	π		π		π		5π
x∊(		,		) lub x∊(		,		)
	6		2		2		6

=============================== k=1

	π		π		π		5π
x∊(		+π,		+π) lub x∊(		+π,		+π)⇔
	6		2		2		6

	7π		3π		3π		11π
x∊(		,		) lub x∊(		,		+π)
	6		2		2		6

=======================================