Optymalizacja Kaparek13 : W stozek o wysokości H i promieniu podstawy R wpisano drugi stozek w ten sposób ze jego wierzchołek leży w środku podstawy danego stożka, a brzeg podstawy leży na powierzchni bocznej. Wyznacz wysokość stożka wpisanego przy której ma on największa objętość. Proszę o pomoc

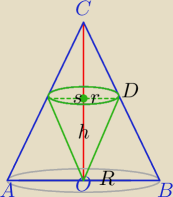
Mila: H=|OC| h=|OS|, h∊(0,H)

	1
V=		πr2*h
	3

1)

	H−h		H		R*(H−h)
ΔDSC∼ΔBOC⇔		=		⇔r=
	r		R		H

	R2*(H2−2H*h+h2)
r2=
	H2

2)

	1		R2*(H2−2H*h+h2)
V(h)=		*		*h⇔
	3		H2

	R2
V(h)=		*(H2*h−2H*h2+h3)
	3H2

3)

	R2
V'(h)=		*(H2−4H*h+3h2)
	3H2

V'(h)=0⇔3h²−4H*h+H²=0 Δ=4H²

	1
h=		H lub h=H ∉D
	3

	1
Dla h=		H funkcja V(h) ma maksimum lokalne
	3

odp.

	1
h=		H
	3

=========== sprawdzaj rachunki