Geometria analityczna, okręgi Gustavo: Dany jest okrąg o równaniu o0: (x−3)²+(y−1)²=1. W pierwszej ćwiartce układu współrzędnych istnieją dwa okręgi o1, o2 styczne zewnętrznie do okręgu o0 i jednoczesnie styczne do obu osi układu współrzędnych. Oblicz odległosc osrodków okregów o1 oraz o2. Ogólnie mam to w kluczu na CKE, więc nie potrzebuję pomocy, mam jednak jedno pytanie. https://cke.gov.pl/images/_EGZAMIN_MATURALNY_OD_2015/egzamin_probny_2015/matematyka_pr/Matematyka_PR_model_odpowiedzi.pdf Strona 17 się zaczyna zadanie. Skąd bierze się przy równaniu (x−r)²+(y−r)²=r²? Wiem, że r to promień, ale dlaczego akurat tak tutaj to działa?

Gustavo: Chodzi o to, skąd się bierze współczynnik r.

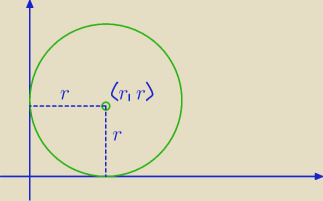iteRacj@: gdyż okrągma środek w punkcie (r,r) i jest styczny do obu osi układu