K Kasia: Damy jest trapez rownoramienny o kącie ostrym 45. Podstawy trapezu są równolegle do osi x, wierzchołki krótszej podstawy należą do paraboli y=−x−5x−2, a ramiona trapezu są odcinkami stycznych do tej paraboli. Wyznacz współrzędne wierzchołków tego trapezu, wiedząc, ze można w niego wpisać okrag.

Kasia: *y=−x²−5x−2

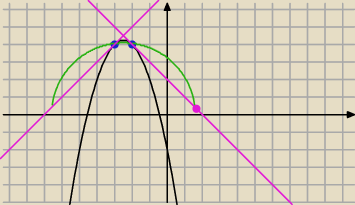
piotr: (−x²−5x−2)' = tg(π/4) ⇒ x=−3 okrąg opisany: y = (67/4−(x+5/2)²)⁽1/2) ramiona: y=−x+2 y=x+7

Kasia: A mógłbyś wytłumaczyć skad To? 😥

piotr: niestety, ale pokręciłem

iteRacj@: okrąg nie jest opisany, ale x₁=−3 współrzędna jednego wierzchołka się zgadza, a równania prostych zawierających boki wyliczone bez okręgu są takie same jak policzyłeś

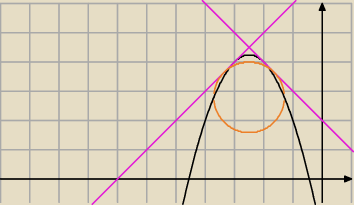
piotr: okrąg wpisany:

3		1
	+		=(x+5/2)2+(y+1/√2−7/2)2
4		√2

piotr: równanie dłuższej podstawy: y = 3−√2