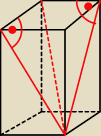
 Podstawą graniastosłupa prostego jest prostokąt o bokach 3 i 4, a wysokość graniastosłupa ma
długość 12. Oblicz sinusy kątów, jakie przekątna prostopadłościanu tworzy z przekątnymi ścian
bocznych mającymi z nią wspólny koniec.
W podpowiedziach mam informację, że kreśląc z tego samego wierzchołka przekątną
prostopadłościanu oraz przekątne ścian bocznych otrzymujemy dwa trójkąty prostokątne,w których
przekątna prostopadłościanu jest przeciwprostokątną.
Po czym powinienem był poznać, że tam są kąty proste?
Podstawą graniastosłupa prostego jest prostokąt o bokach 3 i 4, a wysokość graniastosłupa ma
długość 12. Oblicz sinusy kątów, jakie przekątna prostopadłościanu tworzy z przekątnymi ścian
bocznych mającymi z nią wspólny koniec.
W podpowiedziach mam informację, że kreśląc z tego samego wierzchołka przekątną
prostopadłościanu oraz przekątne ścian bocznych otrzymujemy dwa trójkąty prostokątne,w których
przekątna prostopadłościanu jest przeciwprostokątną.
Po czym powinienem był poznać, że tam są kąty proste?


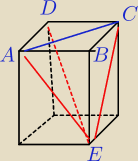 Bez straty ogólności zakładam, że |AB|=3, a |BC|=4
Najpierw policzmy długość |AC|. Z twierdzenia pitagorasa wychodzi, że ma ona dłogość 5.
Teraz możemy policzyć przekątne ścian bocznych.
|AE|2=122+32
|AE|=√153
|CE|2=122+42
|CE|=√160
|CE|=4√10
Oczywiście te równania mają dwa rozwiązania, ale wiadomo, że ani bok ani przekątna nie ma
długości ujemnej.
Policzmy teraz |DE|
Do tego potrzebna nam będzie wysokość która jest równa 12, oraz |DB|, która jest równa |AC|,
czyli 5
Z twierdzenia pitagorasa otrzymujemy długość |DE|=13.
Teraz, użyjemy twierdzenia cosinusów aby obliczyć cosinus kąta DEC, którego nazwę α.
|DC|2=|DE|2+|CE|2−2*|DE|*|CE|*cosα
9=169+160−2*13*4√10*cosα
144√10*cosα=320
cosα=320/144√10
cosα=320√10/1440
cosα=8√10/36
cosα=2√10/9
Korzystając z jedynki trygonometrycznej:
sin2α+cosα=1
sin2α+40/81=1
sin2α=41/81
sinα=√41/9, sinα>0
Z drugim sinusem robisz tak samo
Bez straty ogólności zakładam, że |AB|=3, a |BC|=4
Najpierw policzmy długość |AC|. Z twierdzenia pitagorasa wychodzi, że ma ona dłogość 5.
Teraz możemy policzyć przekątne ścian bocznych.
|AE|2=122+32
|AE|=√153
|CE|2=122+42
|CE|=√160
|CE|=4√10
Oczywiście te równania mają dwa rozwiązania, ale wiadomo, że ani bok ani przekątna nie ma
długości ujemnej.
Policzmy teraz |DE|
Do tego potrzebna nam będzie wysokość która jest równa 12, oraz |DB|, która jest równa |AC|,
czyli 5
Z twierdzenia pitagorasa otrzymujemy długość |DE|=13.
Teraz, użyjemy twierdzenia cosinusów aby obliczyć cosinus kąta DEC, którego nazwę α.
|DC|2=|DE|2+|CE|2−2*|DE|*|CE|*cosα
9=169+160−2*13*4√10*cosα
144√10*cosα=320
cosα=320/144√10
cosα=320√10/1440
cosα=8√10/36
cosα=2√10/9
Korzystając z jedynki trygonometrycznej:
sin2α+cosα=1
sin2α+40/81=1
sin2α=41/81
sinα=√41/9, sinα>0
Z drugim sinusem robisz tak samo
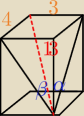 Raczej powinno być tak:
Liczymy przekątną w graniastosłupie d=√32+42+122 = 13
sin α = 3/13
sin β = 4/13
Raczej powinno być tak:
Liczymy przekątną w graniastosłupie d=√32+42+122 = 13
sin α = 3/13
sin β = 4/13
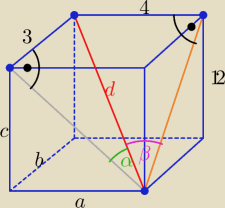 d=√a2+b2+c2= √16+9+144=√169 ⇒ d=13
d=√a2+b2+c2= √16+9+144=√169 ⇒ d=13
| 3 | 3 | 4 | 4 | |||||
sinα= | = | i sinβ= | = | |||||
| d | 13 | d | 13 |
