bryły
małgoś: Na kuli o promieniu R = 3 opisano stożek o możliwie najmniejszej objętości. Oblicz
wysokość oraz promień podstawy tego stożka. Oblicz tę najmniejszą objętość.
30 kwi 17:59
Blee:
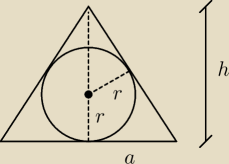
podobieństwo trójkątów i 'jedziesz' z koksem
30 kwi 18:16
Mila:
Oj, koks nie jest zdrowy

30 kwi 18:52
małgoś: nic mi to nie mówi
r=3
| | a | | h | | l | |
mam |
| = |
| = |
| oraz a2+h2=l2 |
| | 3 | | l−a | | h−3 | |
30 kwi 22:01
Mila:
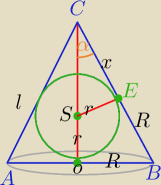
|CO|=H, r=3
1) ΔSEC∼ΔCOB⇔
3H+R
2=R
√H2+R2 /
2
9H
2+6R
2*H+R
4=R
2*(H
2+R
2)
9H
2+6R
2*H+R
4=R
2*H
2+R
4
9H
2+6R
2*H=R
2*H
2 /:H
9H+6R
2=R
2*H
9H=R
2*H−6R
2
R
2*(H−6)=9H, H>6
2)
| | 1 | | 9H | | 3H2 | |
V(H)= |
| * |
| *H= |
| |
| | 3 | | H−6 | | H−6 | |
| | 6H*(H−6)−3H2*1 | | 3H2−36H) | |
V'(H)= |
| = |
| |
| | (H−6)2 | | (H−6)2 | |
V'(H)=0⇔H=12
3H*(H−12)>0 i H∊D
H>12
Dla
H=12 funkcja V(H) osiąga minimum
V(12)=72
R=3
√2
============
Sprawdzaj rachunki
30 kwi 23:38
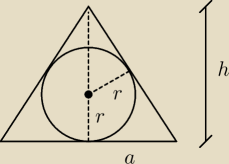 podobieństwo trójkątów i 'jedziesz' z koksem
podobieństwo trójkątów i 'jedziesz' z koksem

 |CO|=H, r=3
1) ΔSEC∼ΔCOB⇔
|CO|=H, r=3
1) ΔSEC∼ΔCOB⇔