helpp pabloo: W trójkąt prostokątny o przyprostokątnych 3 i 4 wpisano nieskończenie wiele kwadratów K1,K2,K3,.. Oblicz sumę pól wszystkich kwadratów.

Krzysiekmatura: 6

Blee: Skoro ma być ich nieskończenie wiele, to ... suma obwodów tych kwadratów = 4*P_Δ

Eta:

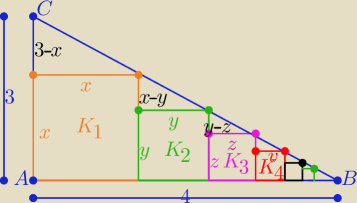
	3
Z podobieństwa trójkątów (małych) do trójkąta ABC w skali k=
	4

	3−x		3		12		12
K1 :		=		⇒ x=		to P(K1)= (		)2
	x		4		7		7

	x−y		3		4		12		4		12
K2:		=		⇒ y=		*		to P(K2)= (		)2*(		)2
	y		4		7		7		7		7

	y−z		3		4		12		4		12
K3 :		=		⇒ z= (		)2*		to P(K3)= (		)4*(		)2
	z		4		7		7		7		7

: : Wartości pól tworzą szereg geometryczny zbieżny

	12		4
a1=(		)2 i q=(		)2 , |q|<1
	7		7

	a1		144   49		144		48
to S=		⇒ S=		=		=
	1−q		16   1−   49		49−16		11

	6
S=4
	11

========

Eta:

	4
Oczywiście ma być : 4
	11

iteRacj@: taki pochód kolorowych kwadratów... (pochód pierwszomajowy oczywiście)

Eta: Brakuje jeszcze chorągiewek