Trzy zadania maturki rozszerzonej na poziomie szkoły średniej Franek: Witam, dałby ktoś rade rozwiązać te 3 zadanka? Z góry dziękuję <3 https://imgur.com/bL5Hj0s https://imgur.com/bfMVluS https://imgur.com/cVWKtxA

aniabb: zadanie 2 podstawiasz pierwszy i trzeci za x odejmujesz stronami a=−2,5 więc b=1,5 min to −1/16 dla x=±√5/2

Franek: Dziękuję za drugie <3

aniabb: pierwsze powinno się dac wzorem Herona https://matematykaszkolna.pl/strona/503.html wiedząc że środkowa dzieli Δ na 2 równe pola

Mila: Liczę pierwsze .

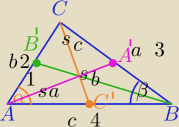
Mila: Suma długości środkowych trójkąta. 1) WΔABC: a²=b²+c²−2*b*c*cosα⇔3²=2²+4²−2*2*4*cosα

	11
cosα=
	16

b²=c²+a²−2*a*c*cosβ⇔ 2²=4²+3²−2*3*4cosβ

	7
cosβ=
	8

2) W ΔABB' :

	11
sb2= 12+42−2*1*4*
	16

	23
sb2=
	2

	√46
sb=
	2

=========== 3) W ΔAC'C:

	11
sc2=22+22−2*2*2*
	16

	5
sc2=
	2

	√10
sc=
	2

========== 4) W ΔABA':

	7
sa2=42+1.52−2*4*1.5*
	8

s_a²=7.75

	√31
sa=
	2

===================== 5) Suma:

	√31+√46+√10
s=
	2

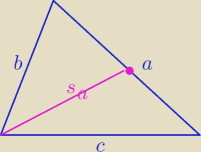Eta: https://pl.wikipedia.org/wiki/%C5%9Arodkowa_tr%C3%B3jk%C4%85ta

	1
sa=		√2b2+2c2−a2
	2

	1		√31
sa=		√8+32−9=
	2		2

Mila: Tak liczyłam, ale nie wiem, czy mają wyprowadzone wzory w szkole.