geometria i równanie z uzasadnieniem odpowiedzi Marcin: 1. Uzasadnij, że w dowolnym pięciokącie wypukłym istnieją trzy przekątne, z których można zbudować trójkąt. 2. Ile pierwiastków rzeczywistych ma równanie (√3–1)^x = (2(√2+1)^x)+1? Uzasadnij odpowiedź.

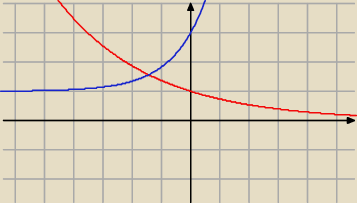
Adamm: 2. f(x)=(√3−1)^x − maleje g(x)=2(√2+1)^x+1 − rośnie mogą się przecinać jedynie w jednym miejscu i faktycznie się przecinają, bo g(−2)<f(−2), g(0)>f(0), a funkcje g, f są ciągłe