Oblicz promień okręgu Domek: Oblicz promień okręgu opisanego na trójkącie, jeżeli boki trójkąta mają długości 10 i 4√3, a kąt między nimi ma 150° Źle wychodzi mi to zadanie, proszę o pomoc

Mila: Obliczyłeś długość trzeciego boku?

Domek: z tw. cos niby wyszło mi 2√67, ale to jest chyba źle

Lech: Z twierdzenia cosinusow oblicz trzeci bok trojkata , nastepnie oblicz pole trojkata i nastepnie promien okregu opisanego na trojkacie , sa na to gotowe wzory ! ! Popatrz do karty wzorow !

Mila: Dobrze.

2√67
	=2R
sin(150)

√67
	=R
sin30

R=2√67 Inną masz odpowiedź?

La gringa: Wszystko pięknie wychodzi z zastosowaniem twierdzenia cosinusów x − długość boku naprzeciwko kąta α=150. x² = 10² + (4√3)² − 2*10*4√3*cos(α) x² = ..... cos(α) zamieniamy na sinus korzystając z odpowiednich wzorów. wychodzi nam długość trzeciego boku. A potem odpowiednio korzystam y z wzoru na pole trójkąta znając długość jego wszystkich boków. czyli: P_Δ = √p(p−a)(p−b(p−c) gdzie p − połowa długości obwodu trójkąta.

	a*b*c
A potem obliczone pole podstawiamy do wzoru na inne pole trójkąta: PΔ =
	4R

Gdzie R to nasz szukany promień.

Lech: Pole trojkata lepiej obliczyc na podstawie wzoru P = (1/2) a * b * sin α

Domek: Mila, tak tyle mi wyszło. Tylko nie mogłem uwierzyć w wnioski, w sensie że 3 bok tego trójkąta jest jednocześnie średnicą. Może to kwestia mojego złego rysunku. No nic dziękuję że mnie upewniliście. Jesteście ekstra <3

Eta: Bez obliczania pola !

	c
z tw. sinusów 2R=
	sin150o

Lech: Tak , Eta ma racje ! ! Mila rowniez ! !

Mila: Domek Średnica jest równa 4√67.

Domek: sorry miałem na myśli promień :3

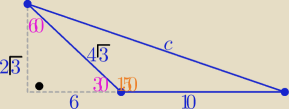
Eta: Można jeszcze tak ( patrz rys.) z trójkąta "ekierki" i tw. Pitagorasa c²=(2√3)²+16²= 268 = 6*67 ⇒ c=2√67

	abc		10*4√3*2√67
R=		=		= 2√67
	4P		4*5*2√3

Domek: Też ciekawe rozwiązanie Eta Dzięki