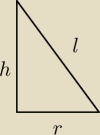
Optymalizacja Adam: Rozpatrujemy wszystkie stożki o tworzącej długości L. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.

	1
V=		πr2h
	3

Z tw. Pitagorasa r²+h²=l² ⇒ h=√l²−r² D: r∊ (0,l) dobrze jest to policzone?

	1		1		1
V(r)=		πr2h=		πr2√l2−r2=		π√l2r4−r6
	3		3		3

To co znajduje się przed ułamkiem nie ma wpływu na wartość r dla którego ta funkcja osiąga maksimum. f(r)=l²r⁴−r⁶

	6		√6		√6
f'(r)=4l2r3−6r5=4r3(l2−		r2)=4r3(l+		r)(l−		r)
	4		2		2

	√6
I wyszło mi że max jest dla		r
	2

Czy dobrze robię to zadanie?

iteRacj@: warunek r∊ (0,l) dobrze, dodaj jeszcze h∊ (0,l)

	√6
popraw wynik: l−		r=0
	2

musisz napisać, że dlaczego dla tej wartości r funkcja f(r) osiąga maksimum

iteRacj@: popraw wynik, bo trzeba wartość r uzależnić od l

La gringa: Ogólnie rozumowanie poprawne ale zaczynasz się gubić w wyznaczaniu pochodnej/uzależniania od stałej. A przynajmniej tak mi się wydaje, ale nie oceniam, gdyż pewnie nawet tutaj w tej wypowiedzi zrobię błąd xD Tak czy inaczej do momentu wyznaczenia funkcji V(r) zrobiłabym identycznie. a następnie: Zał. r>0; i r < L czyli w sumie r∊(0;L) h>0; L>0;

	π
f(r)=		* √L2r4−r6
	3

	π		1
f'(r)=		*		* (L2*r4−r6)'
	3		2*√L2r4−r6

	π		L2*4r3 − 6r5
f'(r) =		*		← nasza pochodna.
	3		2*√L2r4−r6

Liczymy dla jakiego r będzie maksimum (ekstrema) f'(r) = 0 ← warunek konieczny.

	π		L2*4r3 − 6r5
0 =		*		/ * 6*√L2r4−r6
	3		2*√L2r4−r6

0 = π*(L²*4r³ − 6r⁵) / :π 0 = L²*4r³ − 6r⁵ 0 = r³(L²*4 − 6r²) r₀=0 nie speł założeń. lub 6r² = 4L²

	2
r2=		L2 / √
	3

	√2*L		√6*L		√2*L		√6*L
r1 =		=		lub r2 = −		=−		nie spełnia
	√3		3		√3		3

założeń. Warunek wystarczający: (rys powyżej) Spełniony. Czyli maksimum osiąga dla r₁. Potem podstawiamy nasze r₁ do wzoru na h = √L² − r² i objętość stożka. I mamy odp na nasze zadanie. Ogólnie w zadaniach optymalizacyjnych trzymać się trzeba stałej oznaczonej w treści zadania u nas jest to L. I to od niej uzależniać zmienne typu r lub h.

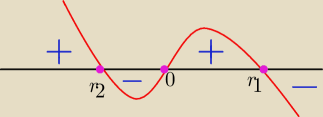
La gringa: Oczywiście napisałam "rysunek powyżej" a rysunku nie dołączyłam XDDDD) + tak jak napisał iteRacj@ trzeba jeszcze dodać że h ∊ (0;L) o którym to zapomniałam xd