Dana jest funkcja f(x) = |x+4|-|x-2|, gdzie x należy do zbioru liczb rzeczywisty signumy: Dana jest funkcja f(x) = |x+4|−|x−2|, gdzie x należy do zbioru liczb rzeczywistych. a) Naszkicuj wykres tej funkcji. b) Podaj jej miejsca zerowe. c) Określ liczbę rozwiązań równania f(x) = m w zależności od parametru m.

Blee: I problem polega na? Funkcje ta rozpatrujesz na trzech przedzialach: x<−4 x∊<−4,2> x>2 Jak ta funkcja wyglada w kazdym z tych przedzialow?

signumy: Głównie na punkcie c

La gringa: Jak chodzi o podpunkt c) to rysujesz po prostu wykres tej funkcji i potem prostą. I przesuwasz ją po utworzonym wykresie i zliczasz ilość rozwiązań.

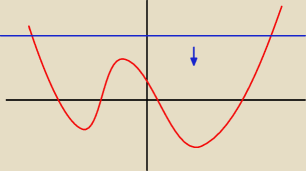
La gringa: W stylu jak na obrazku (wykres funkcji jest przykładowy)

signumy: Mogę prosić o napisanie przykładowego rozwiązania?

Blee: Przykladowe rozwiazanie: c) Dla m > 6 −−− brak rozwiazan Dla m = 6 −−− nieskonczenie wiele rozwiazan Dla m ∊ (−6 , 6) −−− jedno rozwiazanie Dla m = −6 −−− nieskonczenie wiele rozwiazan Dla m<−6 −−− brak rozwiazan

La gringa: f(x) = |x+4| − |x−2| funkcja zależy od przedziałów. czyli f(x) = { −(x+4) − (−(x−2)) dla x∊(∞;−4) (x+4) − (−(x−2)) dla x∊ <−4;2) (x+4) − (x−2) dla x∊<2;∞) } Po redukcji wyrazów podobnych widać że są to funkcję liniowe. Wyznaczasz sobie po 2 punkty z każdego przedziału i podstawiasz do odpowiedniego wzoru z przedziału. Rysujesz te funkcje liniowe. Odczytujesz miejsca zerowe. Następnie rysujesz prostą o równaniu y=m. I patrzysz dla jakiego m i w ilu miejscach ta prosta przecina narysowany przez Cb wykres. (np. dla m=3 prosta przecina wykres w 5 miejscach. Czyli dla m=3 Mamy 5 rozwiązań.) I przesuwasz tą prostą od góry do dołu wykresu.

signumy: A tak! Teraz już rozumiem! Dziękuję wszystkim za pomoc