trójkaaty Kluska: Dany jest trójkat ABC, punkty P,Q,R leżą odpowiednio na BC,CA,AB tak że BP: PC=CQ:QA=AR:RB=m:n. Pokaż że stosunek pól trójkatów PQR oraz ABC wynosi (m³+n³):(m+n)³

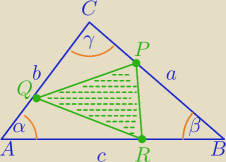
Mila: P_ΔABC=S

	m
k=		( załóżmy, że m>n )
	n

	BP
1)		=k⇔|BP|=k*|PC| stąd: |PC|+k*|PC|=a,
	PC

	1		k
|PC|=a*		, | BP|=a*
	1+k		1+k

	CQ
2)		=k liczymy w podobny sposób
	QA

	k		1
|CQ|=b*		, |AQ|=b*
	1+k		1+k

3)

AR		k		1
	=k⇔|AR|=c*		, |BR|=c*
BR		1+k		1+k

============================

	1		1		k		1
4) PΔARQ=		*|AR|*|AQ|*sinα=		c*		*b*		*sinα=
	2		2		1+k		1+k

	k
=		*S
	(1+k)2

	k
PΔRBP=		*S
	(1+k)2

	k
PΔPQC=		*S
	(1+k)2

Suma tych pól:

	3k
S3=		*S
	(1+k)2

5)

	3k		3k
PΔPQR=S−		*S=S*(1−		=..
	(1+k)2		(1+k)2

	m
Podstawiamy k=
	n

	3m   n		3mn
=S*(1−		)=S*(1−		)=
	m   (1+ )2   n		(m+n)2

	m2+2mn+n2−3mn
=S*
	(m+n)2

PΔPQR		m2−mn+n2
	=
S		(m+n)2

⇔podanej postaci

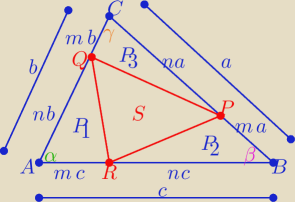Eta: Podobnie .... ale bez "k" |AB|=(m+n)*c , |BC|=(m+n)*a, |AC|=(m+n)*b

	(m+n)2*cb*sinα		(m+n)2*ac*sinβ		(m+n)2*ab*sinγ
S=P(PQR) P=P(ABC)=		=		=
	2		2		2

S= P−(P₁+P₂+P₃)

	mncb*sinα		mn		mn		mn
P1=		=		*P=P2...... =		*P=P3=		*P
	2		(m+n)2		(m+n)2		(m+n)2

	P		P		m+n
to S=		(m+n)2−3mn)=		(m2−mn+n2) /*
	(m+n)2		(m+n)2		m+n

	P(m3+n3)
S=
	(m+n)3

	S		m3+n3
zatem		=
	P		(m+n)3

==========