Rozwiąż nierówność. Założenia, objaśnienie.
La gringa:
√x−5 ≥ 11 − x
zał. x−5 ≥ 0 ⇒ x ≥ 5
√x−5 ≥ 11 − x / ()
2
x−5 ≥ (11−x)
2
0 ≥ x
2 − 23x + 126
Δ = 25
√Δ = 5
x
1 = 9,
x
2 = 14
czyli z uwzględnieniem założenia x≥5 otrzymuję: x∊<9;14>.
Jednak patrząc na rozwiązanie graficzne na wolframie odpowiedzią powinno być <9;
∞).
Moje pytanie brzmi: czy zapomniałam o jakimś dodatkowym założeniu w rozwiązywaniu wyżej,
czy może o czymś innym?

27 kwi 12:43
La gringa: Dobra już widzę swój błąd, − przy podnoszeniu do kwadratu musiałabym zrobić osobne przypadki
dla 5≤x≤11 ?
27 kwi 12:46
Blee:
A gdzie zalozenie, ze dla 11−x <0 bedzie to zawsze spelnione (o ile tylko pod pierwiastkien nie
ma ujemnej liczby)

27 kwi 12:59
La gringa:
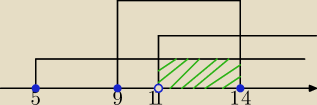
x≥5
x∊<9;14>
x>11
Już się pogubiłam w tej prostej nierówności

27 kwi 13:19
Jack:
√x−5 ≥ 11 − x
założenia:
x−5 ≥ 0 −−> x ≥ 5
Teraz 2 przypadki:
1) 11−x < 0 (wtedy nierownosc jest zawsze spelniona bo po lewej stronie nierownosci pierwiastek
daje liczbe nieujemna a po prawej masz ujemna)
czyli dla x > 11 nierownosc jest zawsze spelniona, wiec mamy juz przedzial :
x ∊ (11;
∞)
2) 11−x ≥ 0 (nierownosc po obu stronach nieujemna, mozna podniesc do kwadratu)
czyli dla x ≤ 11 mamy:
√x−5 ≥ 11 − x /
2
x−5 ≥ 121 − 22x + x
2
x
2 − 23x + 126 ≤ 0
Δ = 25 ,
√Δ = 5
//rysujemy krzywa i mamy rozw. :
x ∊ < 9;14 >
uwzgledniajac zalozenie x ≤ 11 mamy x ∊ <9;11>
sumujac przedzialy
1) i 2) oraz uwzgledniajac zalozenie te z poczatku zadania tzn. x ≥ 5
ostatecznie mamy: x ∊ <9;
∞)
27 kwi 14:12
La gringa: Bardzo dziękuję Jack'u

27 kwi 14:32


 x≥5
x∊<9;14>
x>11
Już się pogubiłam w tej prostej nierówności
x≥5
x∊<9;14>
x>11
Już się pogubiłam w tej prostej nierówności
