katy Eka: W czworokacie ABCD wiemy że AB = 4 − √2, BC = 1 oraz CD = 3, dodatkową kąt ABC = 135^o oraz kąt BCD = 90^o. Oblicz tg∡CDA.

Bogdan:

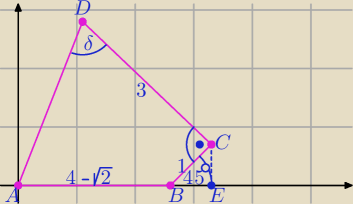
	√2
|BE| = |EC| =
	2

	√2		√2
A = (0, 0), B = (4−√2, 0), C = (4−		,		)
	2		2

prosta BC: y = x − (4−√2), CD⊥BC

	√2		√2
prosta CD: y = −(x − (4−		)) +		⇒ y = −x + 4
	2		2

D = (x_D, y_D) = (x_D, −x_D+4), x_D > 0 i y_D > 0

	√2		√2
|CD|2 = 9 ⇒ (xD − (4−		))2 + (−xD+4 −		)2 = 9
	2		2

x_D = ... i y_D = −x_D + 4 = ...

	yD
tgδ =		= ...
	xD

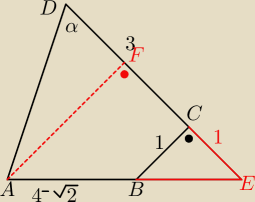an: ∡FAE=∡FEA=45^o CB=CE=1 BE=√2 DE=4 AE=4−√2+√2=4 AF=FE=√8 DF=4−√8

	√8
tgα=		=1+√2
	4−√8