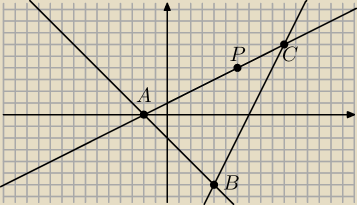
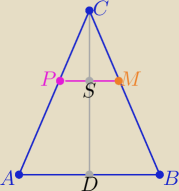
 1/ rozwiązując układ równań prostych AB i BC otrzymasz B(x,y) =.... B(4, −6)
2/ prosta PM ⊥ AB i przechodzi przez P(6,4) oraz AB: y=−x+2
to PM: ma równanie y=(x−6)+4 ⇒ y= x−2
rozwiązując układ równań prostej PM i BC otrzymasz M(8,2)
3/ środek S odcinka PM : S(7,3)
4/ prosta CD ⊥AB : CD: y= −(x−xS)+yS ⇒ CD: y=x−4
rozwiązując układ równań CD i BC otrzymasz C(10,6)
5/ rozwiązując układ równań CD i AB otrzymasz D(1 −3)
6/ xA= 2xD−xB i yA=2yD−yB
xA= −2 i yA=0
A(−2,0)
co zgadza się z rysunkiem Piotra
Odp: A(−2,0), B( 4,−6) , C( 10,6)
========================
1/ rozwiązując układ równań prostych AB i BC otrzymasz B(x,y) =.... B(4, −6)
2/ prosta PM ⊥ AB i przechodzi przez P(6,4) oraz AB: y=−x+2
to PM: ma równanie y=(x−6)+4 ⇒ y= x−2
rozwiązując układ równań prostej PM i BC otrzymasz M(8,2)
3/ środek S odcinka PM : S(7,3)
4/ prosta CD ⊥AB : CD: y= −(x−xS)+yS ⇒ CD: y=x−4
rozwiązując układ równań CD i BC otrzymasz C(10,6)
5/ rozwiązując układ równań CD i AB otrzymasz D(1 −3)
6/ xA= 2xD−xB i yA=2yD−yB
xA= −2 i yA=0
A(−2,0)
co zgadza się z rysunkiem Piotra
Odp: A(−2,0), B( 4,−6) , C( 10,6)
========================
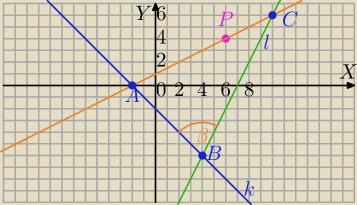 1) rysuję prostą k: y=−x−2
2) rysuję prostą l: y=2x−14
punkt przecięcia: −x−2=2x−14
x=4
y=−6
B=(4,−6)
3) ramiona AC i BC są nachylone do podstawy pod tym samym kątem
k1=−1
k2=2
1) rysuję prostą k: y=−x−2
2) rysuję prostą l: y=2x−14
punkt przecięcia: −x−2=2x−14
x=4
y=−6
B=(4,−6)
3) ramiona AC i BC są nachylone do podstawy pod tym samym kątem
k1=−1
k2=2
| −1−2 | ||
tgβ=| | |=3 tg kąta ostrego między prostą k i l | |
| 1+2*(−1) |
| k3−k1 | ||
3= | ⇔ | |
| 1+k1*k3 |
| k3+1 | ||
3= | ||
| 1−k3 |
| 1 | ||
k3= | ||
| 2 |
| 1 | ||
y= | x +b i P∊prostej | |
| 2 |
| 1 | ||
4= | *6+b⇔b=1 | |
| 2 |
 ]
]
| 1 | ||
y= | x+1 | |
| 2 |
