Trójkąt w którym poprowadzono odcinek równoległy do jednego z boków eM Kej: Dany jest trójkąt, w którym poprowadzono odcinek równoległy do jednego z boków. Ten odcinek podzielił trójkąt na 2 figury o równych polach. W jakim stosunku podzielił bok tego trójkąta?

Mila:

	1
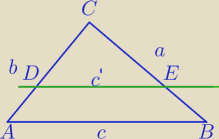
P{ΔDEC}=P=		PΔABC}
	2

	c'
ΔDEC∼ΔABC w skali k=
	c

Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa⇔

PΔDEC		P		1
	=		=
PΔABC		2P		2

1
	=k2
2

	1
k=
	√2

	1		a√2
|CE|=		a=
	√2		2

	a√2
|EB|=a−
	2

CE		a√2   2		√2+1
	=		=
EB		√2   a*(1− )   2		1

eM Kej: @Mila dziękuję uprzejmie

Mila:

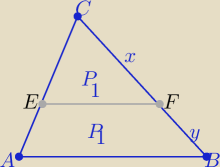Eta: Z podobieństwa trójkątów ABC i EFC w skali k>0

P(ABC)		2P1
	= k2 ⇒		=k2 ⇒ k=√2
P(EFC)		P1

	x+y		y		y
to		=k ⇒ 1+		=√2 ⇒		= √2−1
	x		x		x

===========

Eta:

	x		1
to		=		= √2+1
	y		√2−1

jak podała Mila