Równanie kwadratowe z parametrem Krzyś: Równanie kwadratowe kx² − (k² +4)x +1 = 0 ma dwa różne pierwiastki. Znajdź tę wartość parametru k dla której suma pierwiastków danego równania jest najmniejsza oraz tę wartość parametru k dla której suma pierwiastków tego równania jest największa. Czy to zadanie nie jest źle zrobione? Tak mi się wydaje po próbach rozwiązania

piotr:

	k2+4
S(k) =
	k

piotr: ja bym tu mówił raczej o minimum i maksimum lokalnym max{(k² + 4)/k} = −4 w k = −2 min{(k² + 4)/k} = 4 w k = 2

Tomasz : Ciekawe zadanie. Dobra nie jestem z matmy, ale powiem Ci tak mnie wyszło, że x= 1/4. Później tego x podstawilam do równania i wyszło mi że L=P Pewnie źle mam. Oczywiście wcześniej jeszcze mając ten nawias w równaniu wymnozylam uważając na znaki.

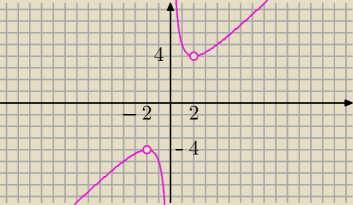
ite: równanie kwadratowe → k≠0 dwa różne pierwiastki dla k∊R\{0} f(k) ma minimum lokalne równe 4 (dla k=2) i maksimum lokalne równe −4 (dla k=−2), ale najmniejsza oraz największa wartość funkcji (a tym samym suma pierwiastków) nie istnieje

Tadeusz: zacznij od Δ

ite: @ Tadeuszzaczęłam od Δ=(k²+2k+4)(k²−2k+4) dodatnia dla każdego k∊R\{0} gdzieś jest błąd?

Tadeusz: dla k<0 ... "parabolka smutna" ... funkacja ma maximum dla k>0 funkcja ma minimum

ite: Ale funkcja opisująca sumę pierwiastków podanego równania nie jest kwadratowa, jest funkcją wymierną (15:05).. Jej wykres nie jest parabolą (bardzo mi się podoba określenie "parabolka smutna" : ).