Optymalizacja
Jasiu: Dwa wierzchołki A i B kwadratu ABCD należą do prostej x−2y=0, a wierzchołek C należy do
| | 8 | |
hiperboli o równaniu y= − |
| . Oblicz długość przekątnej kwadratu, którego pole jest |
| | x | |
najmniejsze.
Obliczyłem pochodną, miejsca zerowe i długość przekątnej, ale nie wychodzi mi narysowanie
wykresy i pokazanie, dla jakich x pochodna jest > 0 etc.
26 kwi 13:05
Jasiu: Podbijam
29 kwi 10:10
29 kwi 10:12
Janek191:
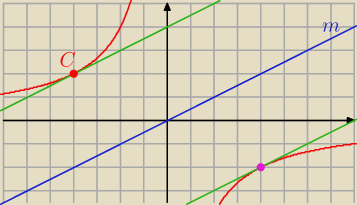
m :y = 0,5 x
Prosta równoległa do m :
y = 0,5 x + b
więc
0,5 x
2 + b x + 8 = 0
Δ = b
2 − 4*0,5*8 = b
2 − 16 = 0 ⇔ b = − 4 lub b = 4
zatem
y = 0,5 x − 4 lub y = 0,5 x + 4
| | 8 | |
Punkt wspólny prostej y = 0,5 x + 4 i hiperboli y = − |
| |
| | x | |
0,5 x
2 + 4 x + 8 = 0
Δ = 16 − 4*0,5*8 = 16 − 16 = 0
29 kwi 13:03
piotr:
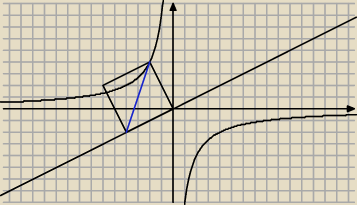
min{(x + 16/x)
2} = 64/5 w x = −4 i x=4
przekątna:
p=8
√2/
√5
29 kwi 13:09
Janek191:
x = − 4
y = 2
C = ( − 4, 2)
Prosta prostopadła do prostej y = 0,5 x przechodząca przez C
y = − 2 x + k
2 = − 2*(−4) + k ⇒ k = − 6
y = −2 x − 6
−−−−−−−−−−−−−−−−
Punkt wspólny tych prostych:
0,5 x = −2 x − 6
2,5 x = − 6
x = − 2,4
y = −1,2
A = ( −2, 4 ; −1,2 )⇔
29 kwi 13:10
Janek191:
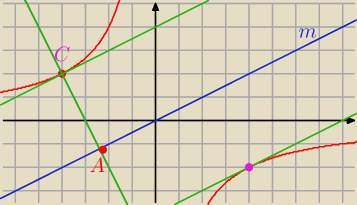
29 kwi 13:24
piotr: w tym zadaniu należy napisać funkcję na pole kwadratu ABCD i znaleźć jej minimum, a nie
zgadywać, że styczna do y=−8/x zawiera bok CD, jak to czyni gość na youtube z podanego linku.
29 kwi 13:24
Janek191:
Zamiast A powinno być B.
29 kwi 13:25
Janek191:
Zadanie rozwiązałem bez korzystania z pochodnej

29 kwi 13:27
piotr: ale gdzie jest wykazanie, że proste y = 0,5 x − 4 lub y = 0,5 x + 4
zawierają boki kwadratu o najmniejszym polu?
29 kwi 13:31
Janek191:
Proste zielone równoległe do prostej y = 0,5 x są styczne do hiperboli, więc
odległość punktu styczności C od punktu B jest najmniejsza.
29 kwi 13:38
 m :y = 0,5 x
m :y = 0,5 x


