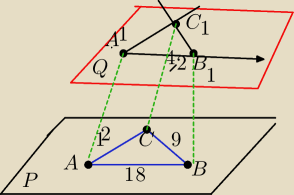
Na plaszczyznie P dany jest trojkat ABC o bokach AB=18 AC=12 BC=9
na plaszczyznie Q rownoleglej do P z dowolnego puntu A1 wykreslono polprosta rownolegla do AB
i na niej odlozono odcinek A1B1 rowny 4,2
Z punktow A1 B1 wykreslono nastepne proste rownolegle odpowiednio do bokow AC i BC Punktem
przeciecia sie tych polprostych jest punkt C1
Obliczyc dlugosci bokow A1 C1 i B1C1 trojkata A1B1C1
| 18 | 30 | |||
ΔABC∼A1B1C1 w skali k= | = | |||
| 4,2 | 7 |
| 7 | ||
|A1C1|=12* | =2,8 | |
| 30 |
| 7 | ||
B1*C1=9* | =2,1 | |
| 30 |
| 30 | ||
Jak doszlas ze to | ? | |
| 7 |
| 18*10 | 180 | 6*30 | |||
= | = | ||||
| 4.2*10 | 42 | 6*7 |