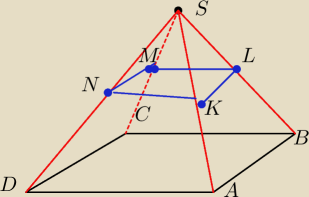
Ostroslup ZKZ: W podstawie jest prostokat − piramida Punkty KLMN to srodki odpowiednich krawedzi Wykazac ze kąt DAB= kątowi NKL Wykazac ze plaszczyzna KLMN jest rownolegla do plaszcyzny podstawy ABCD

ZKZ: Poprawka plaszyzna KLMN przeprowadzona przez proste KLi KN jest... itd

Satan: Środki krawędzi to nic innego, jak środki boków trójkątów. Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku oraz dwa razy mniejszy. Korzystając z tego, że taki odcinek jest równoległy, mamy więc: |KL| || |AB| i analogicznie reszta. Więc skoro odcinki są równoległe, to cała płaszczyzna również. Co do kąta − figury te są podobne. Odpowiednie odcinki KLMN są dwukrotnie mniejsze od odcinków ABCD. Więc kąty przy wszystkich wierzchołkach muszą być równe. Oczywiście mogę się mylić, więc proszę o sprawdzenie mojego rozumowania

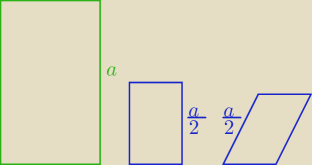
ite: Ja bym dodała jeszcze, że |NL|=1/2*|DB| − to samo tw. : odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i dwa razy od niego krótszy. I skorzystała z ΔDAB≈ΔNKL (bbb). Z tego jednoznacznie wynika, że |< DAB|= |< NKL| Pomysł twierdzenia i dowodu dobry Tylko zauważ, że w czworokącie z równości boków nie wynika równość odpowiednich kątów (dlatego proponuję skorzystanie podobieństwa Δ).

Satan: O, o to właśnie chodziło, o takie sprostowanie Co prawda nie mój temat, ale to ja dziękuję

ZKZ: dziekuje

ite: