Zadanie optymalizacyjne
Adam:
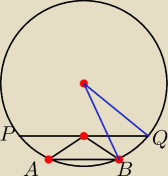
Cięciwa PQ długości 8
√2 podzieliła koło o promieniu 4
√3 na dwa odcinki kołowe.
W odcinek kołowy, który nie zawiera środka koła, wpisujemy trójkąty równoramienne ABC tak
,że podstawa AB jest równoległa do cięciwy PQ, a wierzchołek C jest środkiem tej cięciwy.
Wyznacz długości boków tego z trójkątów, który ma największe pole.
25 kwi 15:08
Adam:
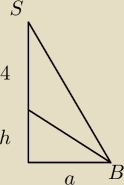
Udało mi się dojść do takiej zależności:
(h+4)
2+a
2=(4
√3)
2
25 kwi 15:10
ite: dobrze rozwiązujesz
PΔ=a*h 0<2a<8√2 0<h<4√3−4
h2+8h+16+a2=48
a2=48−h2−8h−16
a2=−h2−8h+32
PΔ=h√−h2−8h+32 f(h)=√−h4−8h3+32h2
w zadaniu ma być największe pole, więc szukamy h dla którego funkcja f(h) przyjmuje największą
wartość w dziedzinie
a będzie to wtedy gdy funkcja pod pierwiastkiem będzie mieć maksimum
i teraz tego szukasz
25 kwi 15:50
Grześ: Nie da sie bo dlugosci bokow sa niewymierne
25 kwi 22:39
 Cięciwa PQ długości 8√2 podzieliła koło o promieniu 4√3 na dwa odcinki kołowe.
W odcinek kołowy, który nie zawiera środka koła, wpisujemy trójkąty równoramienne ABC tak
,że podstawa AB jest równoległa do cięciwy PQ, a wierzchołek C jest środkiem tej cięciwy.
Wyznacz długości boków tego z trójkątów, który ma największe pole.
Cięciwa PQ długości 8√2 podzieliła koło o promieniu 4√3 na dwa odcinki kołowe.
W odcinek kołowy, który nie zawiera środka koła, wpisujemy trójkąty równoramienne ABC tak
,że podstawa AB jest równoległa do cięciwy PQ, a wierzchołek C jest środkiem tej cięciwy.
Wyznacz długości boków tego z trójkątów, który ma największe pole.
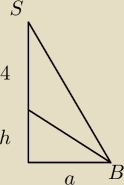 Udało mi się dojść do takiej zależności:
(h+4)2+a2=(4√3)2
Udało mi się dojść do takiej zależności:
(h+4)2+a2=(4√3)2