PLANIMETRIA bluee: Od czworościanu foremnego ABCD o krawędzi 4 odcięto płaszczyzną przechodzącą przez punkt B′ na krawędzi AB, punkt C′ na krawędzi AC i D′ na krawędzi AD ostrosłup AB′C′D′, przy czym |AB′| = 3, |AC′| = 2, |AD′| = 1. a) Oblicz objętość ostrosłupa ABCD i AB′C′D′. b) Oblicz wysokość ostrosłupa AB′C′D′, gdy za jego podstawę przyjmiemy B′C′D′. Podaję link do arkusza maturalnego, gdzie znajduje się zdanie i rysunek. (Zad.15) http://www.zs3.wroc.pl/katalogi/nauczyciele/przedmioty/matematyka/zadania/arkusz%20PR%202015%20w_oszczedna.pdf

	4√32
W podpunkcie A). wyszło mi VABCD=		, ale nie wiem jak obliczyć V tego małego
	3

ostrosłupa...

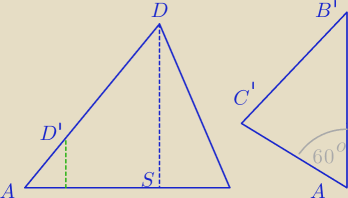
ite: pole podstawy ostrosłupa AB′C′D′ wyliczasz z trójkąta AB′C′ wysokość tego ostrosłupa znajdziesz z proporcji w przekroju dużego ostrosłupa ABCD płaszczyzną przechodzącą przez wierzchołki A i D oraz spodek wysokości S |AD| = 1 |AD′| = 4

ite: |AD'| =1, |AD| = 4

bluee: Mam problem z następnym zadaniem z tego samego testu (zad. 16) Znalazłam je tutaj https://matematykaszkolna.pl/forum/282205.html. Ale ja nie znam twierdzenia Cevy, którego użyto w podpunkcie b). (jestem w liceum). Da się to policzyć jakoś inaczej