Zadanko maturalne 2014 :) matematyczna panika : Rozwiąż nierówność −2sin3x≥1 w przedziale <0,2π> ( proszę o wynik chcę tylko sprawdzić czy mam dobre rozwiązanie)

Blee: to pokaż nam swój wynik ... sprawdzimy, czy dobry masz wynik

matematyczna panika : x∊<7pi/18 11pi/18> ∪ <19pi/18 , 23pi/18> ∪ <31pi/18 , 35pi/18>

Jerzy:

	7π		11π
x ∊ [		;		]
	18		18

matematyczna panika : Czemu reszta wypada ?

Jerzy: Masz zadany przedział : <0;2π>

Jerzy:

	1
I nierówność: sin3x ≤ −		; a to ma miejsce w przedziale: <210;330>
	2

Jerzy: Dobra, moja pomyłka

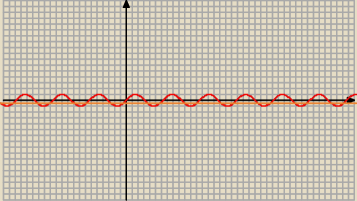
matematyczna panika : Coś czuję że nie do końca rozumiem to zadanie oto moje rozwiązanie: sin3x≤−0,5 dla 3x∊<0,6pi> 3x∊<7pi/6 ,11pi/6> ∪ <19pi/6 , 23pi/6> ∪ <31pi/6 , 35pi/6> x∊<7pi/18 11pi/18> ∪ <19pi/18 , 23pi/18> ∪ <31pi/18 , 35pi/18> dla x∊<0,2pi>

Jerzy: sin3x ∊ <7π/6 + 2kπ ; 11π/6 + 2kπ> ⇔ x ∊ < 7π/18 + 2kπ/3; 11π/18 + 2kπ/3> Teraz podstawiasz pod k liczby calkowite i wyłapujesz kąty z zadanego przedziału.

matematyczna panika : x ∊ < 7π/18 + 2kπ/3; 11π/18 + 2kπ/3> ⇒ x∊< (7pi+12kpi)/18 , (11pi+12kpi)/18> dla x∊<0,2pi> dla k=0 x∊<7pi/18 , 11pi/18> dla k=1 x∊<19pi/18 , 23pi/18> dla k=2 x∊ <31pi/18 , 35pi/18> w sumie x∊<7pi/18 11pi/18> ∪ <19pi/18 , 23pi/18> ∪ <31pi/18 , 35pi/18> czyli się zgadza