dowod johnik: Wykaż, że w dowolnym trapezie do prostej łączącej środki podstaw należy punkt przecięcia przekątnych tego trapezu.

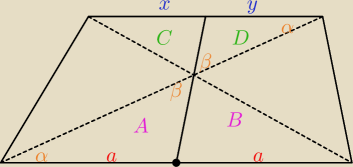
Blee: 1) Wyznaczamy prostą przechodzącą przez przecięcie się przekątnych i środek jednej z podstaw. 2) Musimy wykazać, że przecięcie się tej prostej z drugą podstawą dzieli ów podstawę na połowy. Rozwiązanie: zauważamy (podobieństwo k,k,k −−− co wiemy z odpowiednich tw. odnośnie kątów prostych przecinających się i prostej przecinającej równoległe), że trójkąty A i D oraz B i C są podobne

	PA
w takim razie proporcja pól tych trójkątów także będzie zachowana, tz. :		=
	PB

	PD
		= 1
	PC

Jako, że trójkąty C i D mają taką samą wysokość, to wniosek: x = y c.n.w.