pomocy johnik: W półokrąg o promieniu długości R wpisano trapez, którego podstawą jest średnica okręgu. Dla jakiej miary kata przy podstawie trapezu jego pole powierzchni jest największe ma ktoś plan zeby zapisac to uniknać obliczania pochodnej funkcji trygonometrycznych

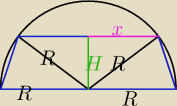
aniabb: R²=H²+x² więc H=√R²−x² P=(x+R)√R²−x²

an: prościej i zgodnie z poleceniem w zadaniu α kąt przy podstawie x=Rcos(180−2α)= − Rcos2α h=Rsin2α P=.... P'=4R²(cos2α−cos4α)=4R²(cos2α−2cos²2α+1)=0 .... α=60^o

jc: Prawie wszystkie tego typu zadania można rozwiązać wykorzystując nierówność pomiędzy średnimi (i pamiętając, że równość mamy tylko dla równych wyrazów). P=(R+x)√R²−x² P² = (R+x)³(R−x)

	R+x		R+x   3 + (R−x)   3
[P2/27]1/4 = [(		)3(R−x)]1/4 ≤		=R
	3		4

Równość mamy w przypadku (R+x)/3=R−x, czyli dla x=R/2.

jc: Jeszcze prościej. Uzupełniamy rysunek drugim trapezem poniżej średnicy. Jeśli skądinąd wiemy, że największe pole wśród sześciokątów wpisanych w okrąg ma sześciokąt foremny, to odpowiedź jest oczywista.