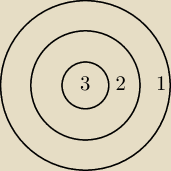
Uczestnik turnieju rzuca rzutkami do tarczy o punktach przyznawanych
tj. na rys. obok (promienie danych okręgów są w odpowiednio w stosunku 1:2:3)
(Trzy okręgi w sobie najmniejszy w środku więc policzyłem że maja pola odpowiednio 1π, 3π,5π)
Wiemy, że zawsze trafia w tarczę.
Jakie jest prawdopodobieństwo, że suma uzyskanych przez zawodnika punktów będzie wynosić
dokładnie 6,
pod warunkiem, że w pierwszym rzucie zdobędzie 2 punkty.
A 17/27α
B 19/27
C 1/3
D 13/27
| 1 | ||
P1 = | ||
| 9 |
| 3 | ||
P2 = | ||
| 9 |
| 5 | ||
P3 = | ||
| 9 |
| 5 | 1 | 1 | 5 | 3 | 3 | 19 | ||||||||
P(A∩B) = | * | + | * | + | * | = | ||||||||
| 9 | 9 | 9 | 9 | 9 | 9 | 81 |
| 3 | 1 | |||
P(B) = | = | |||
| 9 | 3 |
| 19 | 19 | ||||||||||
P(A|B)= | = | *3 = | ||||||||||
| 81 | 27 |
| 3 | ||
P(A∩B) = | *(to co wyżej) | |
| 9 |
| 19 | ||
P(A|B) = | ||
| 81 |