TRAPEZ bluee: Udowodnij, że czworokąt mający kolejne boki o długości 21, 15, 7 i 13 może być trapezem. Oblicz jego pole. Znalazłam takie rozwiązanie: Wystarczy zauważyć ,że za podstawy tego udowadnialnego trapezu przyjmuję odcinki 21 , 7. Rozbijam dolną podstawę 21 na dwa odcinki 21=7+14 . Buduję równoległobok o bokach 7 , 13 , który dopełnię do trapezu. Wtedy jedno z ramion trapezu ( powiedzmy lewe) ma 13 . Oczywiście kąt przy podstawie tego równoległoboku może się zmieniać od (0∘,180∘) . Wtedy dostaję całą rodzinę trapezów dopełniając prawe ramię trapezu długością n . Tak ,że istnieje Δ o bokach 13,14,n . Co zachodzi gdy n∈(1,27) Oczywiście n=15∈(1,27) Jednak za bardzo nie rozumiem tego n∈(1,27)

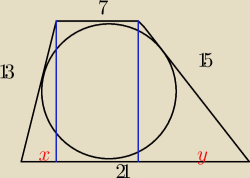
Mo: Wydaje mi się, że można skorzystać z tego, że jeśli da się wpisać okrąg w takich czworokąt, bo zachodzi równość 13 + 15 = 7 + 21, to może być to trapez, choć nie mam pewności czy tyle wystarczy by tak sądzić. A pole obliczyć z Pitagorasa z układu równań.

bluee: Też o tym myślałam... Nie wiem czy to wystarczy, ale tak czy siak dzięki.

q: to ne(1;27) to z nierówności trójkąta ..trzeci bok nie może być dłuższy niż suma dwóch

PW: Spróbuj wykorzystać metodę współrzędnych. Niech podstawa o długości 21 ma końce A=(−10,5, 0) oraz B=(10,5, 0). Punkty C i D muszą leżeć na okręgach o środku A i promieniu 15 oraz o środku B i promieniu 13. Pokazać, że istnieją takie C i D, które mają jednakowe drugie współrzędne (bo CD||AB) i pierwsze współrzędne różniące się o 7.

an: h²=13²−x²=15²−(14−x)² ⇒x=5 y=14−5=9 h=12