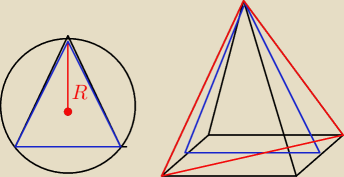
Pytanie Stereometria Pawiuszek: Krawędź boczna ostrosłupa prawidłowego czworokątnego wpisanego w kulę o promieniu R tworzy z płaszczyzną podstawy kąt α. Oblicz pole powierzchni całkowitej tego ostrosłupa. Na literach ciężko stwierdzić czy wyszła mi dobra odp. Czy muszę to opisać tak jak czerwonymi liniami czy moge tak jak niebieskie ?

Pawiuszek: albo chociaż napiszę jakbym robil dla czerwonego czyli po przekątnej lecąc. Czy dobrze ? Na poczatku wyliczam H za pomocą tgα. Teraz korzystam z twierdzenia sinusów i obliczam dzięki temu a. Obliczam dłg krawedzi. a następnie obliczam z pitka wysokosc sciany bocznej. Teraz licze Pole całkowite. Dobrzę robie ? Zgadza się wszystko czy cos poplątałem bo wynik ciężko sprawdzić na literach. A obliczeń 2 kartki Z góry dzięki.

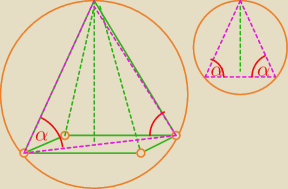
ite: Twój pierwszy rysunek z niebieskim przekrojem nie jest dobry

Pawiuszek: Dziękuję slicznie, czyli opis postępowania równiez jest prawidłowy prawdy ?

ite: czy w zadaniu masz podane R i α? nie wiem z czego wyliczasz H

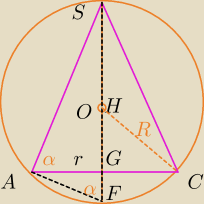
ite: H −wysokość ostrosłupa r − promień podstawy ostrosłupa R − promień kuli można skorzystać z tego przekroju przy liczeniu |FS|=2R, |GS|=H, |GF|=2R−H ΔSAG≈ΔAGF

Pawiuszek: tak alfa jest między krawędzią boczną a plaszczyzna podstawy oraz mam podane R. U góry jest polecenie. H wyliczam z tgα= H/ a√2/2. To H wyraża mi się w a, ale później uzywam tw sinusów. Chyba ok, prawda ?

Pawiuszek: A jeszcze pytanko skąd można wywnioskowac że przy F jest też α. Bo jakoś ja tego nie mogę zobaczyć

ite: <SAF=90^o <SAG=α , <ASG=90^o−α <SFA=90^o−(90^o−α)=α sprawdź wynik zadania z odpowiedziami, bo tak w ciemno (bez podanych odcinków) nie umiem odpowiedzieć, czy dobrze stosujesz tw. sunusów.