PLANIMETRIA bluee: W trapezie ABCD o podstawach AB i CD zawierają się odpowiednio w dwusiecznych kątów BAD i ABC. Uzasadnij, że trapez ABCD jest trapezem równoramiennym.

ite: Jeśli to przekątne trapezu zawierają się odpowiednio w dwusiecznych kątów <BAD i <ABC, to takie zadanie niedawno było.

bluee: Też mi się tak wydawało, ale nie mogę go znaleźć i nie pamiętam rozwiązania...

ite: Albo skorzystaj z twierdzenia o dwusiecznej w trójkątach ΔABC i ΔABD i z podobieństwa ΔABE i ΔCDE. E to punkt przecięcia przekątnych.

bluee: Wyszło mi, że

|CB|		|DC|
	=
|AB|		|AD|

bluee: I co dalej

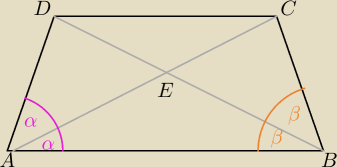
ite: z twierdzenia o dwusiecznej w trójkątach ΔABC i ΔABD

|AE|		|CE|
	=
|AB|		|CB|

|DE|		|BE|
	=
|AD|		|AB|

z podobieństwa ΔABE i ΔCDE

|DE|		|CE|
	=
|EB|		|AE|

pozamieniaj miejscami odcinki w dwóch pierwszych proporcjach

bluee: Dzięki

ite: i o jedno zadanie do matury bliżej