Stereometria
OVDC:
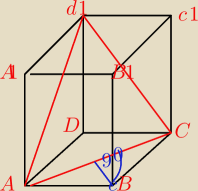
Dany jest sześcian o krawędzi długości a. Oblicz odległość punktu B od płaszczyzny ACD1.
Czy to co mam wyliczyć to jest właśnie niebieska linia?
24 kwi 11:19
OVDC: | | a√2 | |
Niebieskie to mój pomysł, ale odpowiedz |
| jest zbyt prosta |
| | 2 | |
24 kwi 11:20
24 kwi 11:23
OVDC: Nie wiem, nie znam odpowiedzi, też nie jestem pewien czy to o tą odległość chodzi autorowi
zadania
24 kwi 11:28
Pawiuszek: podbijam o rozwiązanie

24 kwi 11:48
Pawiuszek:
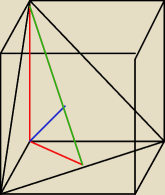
Jednak ja się pokuszę rozwiązać. Na poczatku liczysz zieloną wysokosc. Pozniej obliczasz pole
czerwono zielonego trojkata. Nastepnie to pole przyrownujesz i liczysz wyskosc niebieską i
wlasnie ta wysokosc to odleglosc. Na boku D jest to lepiej widoczne niż na boku B
24 kwi 11:54
Pawiuszek: odp a*
√3/3 jest poprawna

24 kwi 11:55
Pawiuszek: Troszkę pomogłem sobie internetem, ale teraz nurtuje mnie pytanie dlaczego odlegosc od pkt D do
plaszczyzny jest rowna odleglosci B do plaszczyzny, Przeciez ta plaszczyzna jest nachylona
bardziej w jedna ze stron? ?
24 kwi 12:03
ite: to co jest zaznaczone o 11:19 to odległość punktu B od przekątnej AC
a nie jego odległość od płaszczyzny ACD1
24 kwi 12:12
Pawiuszek: ite A dlaczego jest tak jak napisalem wyżej? Wie ktoś i moglby wytlumaczyć

24 kwi 12:15
ite:
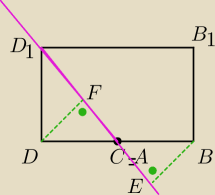
tutaj punkt A jest widoczny jako pokrywający się z C
na tym przekroju widać odległość punktu B od płaszczyzny ACD
1
jest to długość zielonego przerywanego odcinka
|EB| = |DF| gdyż ΔDFC≡ΔCEB (kbk)
łatwiej obliczyć |DF| to ten niebieski odcinek z rysunku o 11:54
24 kwi 12:22
ite: o 11:54 bardzo dobrze zaznaczyłeś szukaną odległość,
to wynika z przystawania trójkątów (opisane powyżej)
24 kwi 12:26
ite:
do znalezienia odległości punktu od płaszczyzny potrzebujemy odcinka należącego do prostej
prostopadłej do tej płaszczyzny
takimi prostymi są DF i EB,
prosta BD nie jest prostopadła do płaszczyzny ACD1
24 kwi 12:31
Mila:
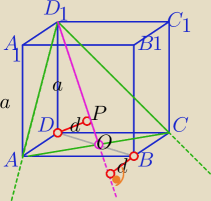
d=?
| 1 | | a√2 | | 1 | | a√6 | |
| a* |
| = |
| * |
| *d |
| 2 | | 2 | | 2 | | 2 | |
==========
24 kwi 19:32
 Dany jest sześcian o krawędzi długości a. Oblicz odległość punktu B od płaszczyzny ACD1.
Czy to co mam wyliczyć to jest właśnie niebieska linia?
Dany jest sześcian o krawędzi długości a. Oblicz odległość punktu B od płaszczyzny ACD1.
Czy to co mam wyliczyć to jest właśnie niebieska linia?

 Jednak ja się pokuszę rozwiązać. Na poczatku liczysz zieloną wysokosc. Pozniej obliczasz pole
czerwono zielonego trojkata. Nastepnie to pole przyrownujesz i liczysz wyskosc niebieską i
wlasnie ta wysokosc to odleglosc. Na boku D jest to lepiej widoczne niż na boku B
Jednak ja się pokuszę rozwiązać. Na poczatku liczysz zieloną wysokosc. Pozniej obliczasz pole
czerwono zielonego trojkata. Nastepnie to pole przyrownujesz i liczysz wyskosc niebieską i
wlasnie ta wysokosc to odleglosc. Na boku D jest to lepiej widoczne niż na boku B


 tutaj punkt A jest widoczny jako pokrywający się z C
na tym przekroju widać odległość punktu B od płaszczyzny ACD1
jest to długość zielonego przerywanego odcinka
|EB| = |DF| gdyż ΔDFC≡ΔCEB (kbk)
łatwiej obliczyć |DF| to ten niebieski odcinek z rysunku o 11:54
tutaj punkt A jest widoczny jako pokrywający się z C
na tym przekroju widać odległość punktu B od płaszczyzny ACD1
jest to długość zielonego przerywanego odcinka
|EB| = |DF| gdyż ΔDFC≡ΔCEB (kbk)
łatwiej obliczyć |DF| to ten niebieski odcinek z rysunku o 11:54
 d=?
d=?