pochodne mk: Funkcja f określona wzorem f(x)=(x−a)(x²−1), gdzie a jest liczbą, osiąga minimum w punkcie

	1
x0=		. Wyznacz maksimum lokalne funkcji f.
	9

Obliczyłam pochodną f'(x)=3x²−2ax−1 Δ=4a²+12 √Δ=2√a²+3

	2a+2√a2+3		1		1
i z tego dwa pierwiastki		=		(bo ramiona są skierowane do góry a
	6		9		9

to minimum lokalne) wychodzi mi z tego równanie 3a+3√a²+3=1 i nie wiem jak to dalej robić, a może coś po drodze mam źle?

Adamm: nie osiąga maksimum, to jest wielomian 3 stopnia

Adamm: minimum*

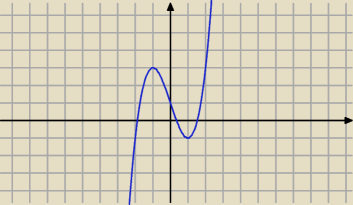
iteRacj@: może mieć i maksimum i minimum ? ?

iteRacj@: lokalne

mk: Czyli jak w końcu?

iteRacj@: według mnie funkcja ma maksimum lokalne x=−3, ale niech się wypowie Adamm, bo mogę sie mylić